In this revision, the authors have made a number of the changes I and the reviewers asked for and I think the paper has improved as a consequence. But there is still one major issue, which the authors have not adequately addressed. This relates to how the model builds on previous work, in particular McNamara et al. 2008. Reviewer 2 had pointed out in their review that it was unclear why the current model yields different results than McNamara et al, specifically, why McNamara et al do not get runaway in their model (and sometimes get efficient outcomes). The authors in their reply make it sound like this is purely a modeling artifact, b/c McNamara et al constrain cooperation (with linear costs and benefits) to be limited to a finite value. But this is clearly incorrect from Figure 3b of McNamara et al: it is true that for some parameter values the ES value of cooperation effort seems cut off at the boundary, but clearly for others there is an internal ESS that is not at the boundary.

This seemingly little detail about the discussion of McNamara et al made me look at their paper more closely, and realize that their model has two very crucial elements completely missing from the current work: (a) in McNamara et al, agents experience constant mortality across their lives (and also it’s an overlapping generations model), (b) in McNamara et al, agents’ current accept/reject decisions affects the supply of future partners. Both of these factors will work against run-away choosiness. I think these crucial differences need to be discussed in detail. Currently, they aren’t mentioned at all and lead me — as well as the reviewers— think that there was a much closer semblance between the current work and McNamara et al. Substantively, they also make me less convinced about the bold statements about how “fixed” partner choice will always run away (which I already thought were somewhat overstated).

On to the gritty details: the neglect of mortality in the current model basically amounts to no discounting of future payoffs. If there is a positive probability that I die before I get to choose again (and therefore leave no offspring), I will be more motivated to take a lower current match and get some payoff rather than have no payoff. This should reduce my choosiness threshold. Even if you don’t think about literal mortality, humans (and other animals) clearly value present rewards more than future ones. The authors remove this discounting completely, and therefore create an unrealistic scenario that promotes the run-away dynamics.

The second piece important difference between the current model and McNamara et al is that if you are choosy and reject a match, chances are your next match is going to be worse. This is because the high quality individuals will not have been rejected, so the supply of new partners will be skewed towards lower quality individuals. This is true even in an infinite population, since even if there is always an infinite number of good quality matches, there will be proportionally more bad matches if the good ones are taken, so you’re more likely to encounter the bad quality ones after the initial choice. McNamara et al do take this into account because their life-cycle only pairs individuals that are single (and therefore dismissed or “widowed” or newborn, page 3 of their supplement). The effect of this is also expected to work against run-away choosiness, since rejecting the current partner does not guarantee a better partner in the future (or from a different perspective, the steady state distribution of potential partners is going to be worse quality overall than the underlying distribution of quality). It is not clear whether this effect is taken into account in the agent-based model, since there isn’t really an adequate description of it, or the code, but it seems clear at least the first effect is not there (since there is no mortality parameter anywhere).

In short, both of these effects would likely counteract the run-away dynamics of choosiness, and probably explain why McNamara et al don’t get such a result. It is true that McNamara et al also don’t always get efficient outcomes, but neither do the authors in their model. Rather, their main conceptual argument is only true quantitatively in the “frictionless” market regime (which as per above is actually quite a bit more frictionless than they make it out to be): there, runaway dynamics happen with fixed choice, but efficiency (or something close to it) obtains with plastic choice. Away from that regime, both conclusions are altered depending on parameters, and as I argue above, trying to make a “fair” comparison with McNamara et al would likely strengthen this conclusion.

In conclusion, I still like the contribution of the paper, and believe that the plastic choice aspect is a welcome addition to the discussion of partner choice in the literature. But I think at a minimum the issues above need to be explicitly acknowledged and discussed. As it is, I think the ms creates a misleading view of how it differs from McNamara et al. but more importantly, it also glosses over some biologically/socially important aspects of partner choice that they take into account and the current paper doesn’t. Ideally, one would take into account these two effects as well, but that might involve some substantial new modeling work.

Minor comments: Incidentally, the authors talk (in their SI) of two potential but equivalent implementations of quality variation: one where it doesn’t change through life, and one it “resets” after every interaction. But in fact the two would yield differences, since the latter implementation would not necessarily have this selection effect for the single-pool.

The comment on Akcay and Van Cleve 2012 is also slightly off: what we showed there was in fact that you can build proximate mechanisms (e.g., families of preference functions) that can yield efficiency (or close to efficiency, see our Figure 2) with very low relatedness. So, it is a bit awkward to cite it as showing that one function requires relatedness as contrast to the current paper.

First off, I apologize to the authors that the review process took somewhat longer than anticipated, and thank them for their patience. I have now obtained two detailed reviews from experts in social evolution theory, and evaluated the paper myself. Both reviewers find the paper to be an interesting and potentially valuable contribution, but raise some important issues that the authors need to address. Based on my own reading, I agree with these comments, and have some concerns myself. I found the paper to be a very interesting read, and agree that it introduces a nice twist to the partner choice story for the evolution of cooperation. That said, I think the paper needs a revision in order to better reflect connections to previous work, the specific contribution of this paper, and also explain its results more transparently.

One issue that Reviewer 2* points out, and I agree, that considering quantitative evolution of cooperation (with diminishing benefits and/or increasing costs of cooperation) per se is a relatively weak argument for novelty. I don’t think this is really the authors’ intention, but at times the introduction does read like that is the main contribution. Even the more specific point of focusing on efficiency has been considered before, not least the McNamara et al. paper that looks at it in the precise setting of this paper, as do Akcay and Van Cleve 2012 (where it’s in the title). It’s true that continuous investment models are outnumbered by discrete strategy papers, but if the framing is “most papers ignore these issues,” I think in fairness the papers that don’t ignore them deserve mention in the framing, and the more specific contribution needs to be fleshed out. I think reviewer 2 in particular points to a helpful framing (their second paragraph), where the real contribution is investigating the effects of different mechanisms of choice on the level of cooperation.

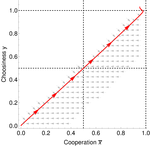
I also find the main narrative of the paper to be somewhat misleading, or at least, incomplete. In particular, the abstract, introduction, and discussion are all state that the “base model” with non-plastic choice generates so much cooperation that it cancels out the benefits. This result is stated unconditionally in most places in the paper (e.g., abstract, l. 21-23, introduction l. 100-102, discussion l. 365-377). But Fig 2 shows that the zero-benefit cooperation result only obtains in the relatively large phenotypic variance limit. At least for medium and high market fluidity, there exists an intermediate level of phenotypic variation where ESS choosiness and cooperation seemingly reach efficient levels. It is true that the variance required to obtain near efficient cooperation is low in absolute value, so perhaps the authors would argue that biologically relevant levels of variance is high relative to these values, but this would need to be spelled out explicitly. As it is, the statements in the lines referenced above strictly speaking false, because they sound like there is an impossibility result, whereas all that there is cooperation evolving to one level or another depending on the parameter set. More generally, it looks like there is quantitative, rather than qualitative differences between the models in how much cooperation can be sustained in equilibrium. So I think this quantitative variation needs to be addressed in a more systematic fashion.

Reviewer 1 and 2 both make a number of useful suggestions in both elucidating the results in more depth and also making the connections to the prior literature more explicit. I think the authors would do well to heed these suggestions. One question I had while reading the model was what would happen if choice was also noisy: after all, in a scenario where cooperation phenotype is noisy, choice being so as well (through errors in perception or execution of choice). In the fixed choice scenario, I can see this further relaxing the constraints to the evolution of cooperation, though intuition is a dangerous guide there. In any case, I feel like this is a relatively straightforward extension of the analysis that would also make the story in this paper more complete.

In sum, I think this has the makings of a nice paper and I think the mechanism proposed here is a nice twist on classic models of partner choice. At the same time, I hope the authors will take these comments at heart and improve the presentation and analysis of their results.

• I am not sure about PCI’s reviewer numbering, but I refer to the plaintext review as Reviewer 1 and the pdf as Reviewer 2)