

Spatial genetic structure, i.e. the non-random spatial distribution of genotypes, arises in populations because of different processes including spatially limited dispersal and selection. Knowledge on the spatial genetic structure of plant populations is important to assess biological parameters such as gene dispersal distances and the potential for local adaptations, as well as for applications in conservation management and breeding. In their work, Niskanen and colleagues demonstrate a multifaceted approach to characterise the spatial genetic structure in two replicate sites of a continuously distributed Scots pine population in South-Eastern Finland. They mapped and assessed the ages of 469 naturally regenerated adults and genotyped them using a SNP array which resulted in 157 325 filtered polymorphic SNPs. Their dataset is remarkably powerful because of the large numbers of both individuals and SNPs genotyped. This made it possible to characterise precisely the decay of genetic relatedness between individuals with spatial distance despite the extensive dispersal capacity of Scots pine through pollen, and ensuing expectations of an almost panmictic population.
The authors’ data analysis was particularly thorough. They demonstrated that two metrics of pairwise relatedness, the genomic relationship matrix (GRM, Yang et al. 2011) and the kinship coefficient (Loiselle et al. 1995) were strongly correlated and produced very similar inference of family relationships: >99% of pairs of individuals were unrelated, and the remainder exhibited 2nd (e.g., half-siblings) to 4th degree relatedness. Pairwise relatedness decayed with spatial distance which resulted in extremely weak but statistically significant spatial genetic structure in both sites, quantified as Sp=0.0005 and Sp=0.0008. These estimates are at least an order of magnitude lower than estimates in the literature obtained in more fragmented populations of the same species or in other conifers. Estimates of the neighbourhood size, the effective number of potentially mating individuals belonging to a within-population neighbourhood (Wright 1946), were relatively large with Nb=1680-3210 despite relatively short gene dispersal distances, σg = 36.5–71.3m, which illustrates the high effective density of the population.
The authors showed the implications of their findings for selection. The capacity for local adaptation depends on dispersal distances and the strength of the selection coefficient. In the study population, the authors inferred that local adaptation can only occur if environmental heterogeneity occurs over a distance larger than approximately one kilometre (or larger, if considering long-distance dispersal). Interestingly, in Scots pine, no local adaptation has been described on similar geographic scales, in contrast to some other European or Mediterranean conifers (Scotti et al. 2023).
The authors’ results are relevant for the management of conservation and breeding. They showed that related individuals occurred within sites only and that they shared a higher number of rare alleles than unrelated ones. Since rare alleles are enriched in new and recessive deleterious variants, selecting related individuals could have negative consequences in breeding programmes. The authors also showed, in their response to reviewers, that their powerful dataset was not suitable to obtain a robust estimate of effective population size, Ne, based on the linkage disequilibrium method (Do et al. 2014). This illustrated that the estimation of Ne used for genetic indicators supported in international conservation policy (Hoban et al. 2020, CBD 2022) remains challenging in large and continuous populations (see also Santo-del-Blanco et al. 2023, Gargiulo et al. 2024).
CBD (2022) Kunming-Montreal Global Biodiversity Framework. https://www.cbd.int/doc/decisions/cop-15/cop-15-dec-04-en.pdf
Do C, Waples RS, Peel D, Macbeth GM, Tillett BJ, Ovenden JR (2014). NeEstimator v2: re-implementation of software for the estimation of contemporary effective population size (Ne ) from genetic data. Molecular Ecology Resources 14: 209–214. https://doi.org/10.1111/1755-0998.12157
Gargiulo R, Decroocq V, González-Martínez SC, Paz-Vinas I, Aury JM, Kupin IL, Plomion C, Schmitt S, Scotti I, Heuertz M (2024) Estimation of contemporary effective population size in plant populations: limitations of genomic datasets. Evolutionary Applications, in press, https://doi.org/10.1101/2023.07.18.549323
Hoban S, Bruford M, D’Urban Jackson J, Lopes-Fernandes M, Heuertz M, Hohenlohe PA, Paz-Vinas I, et al. (2020) Genetic diversity targets and indicators in the CBD post-2020 Global Biodiversity Framework must be improved. Biological Conservation 248: 108654. https://doi.org/10.1016/j.biocon.2020.108654
Loiselle BA, Sork VL, Nason J & Graham C (1995) Spatial genetic structure of a tropical understorey shrub, Psychotria officinalis (Rubiaceae). American Journal of Botany 82: 1420–1425. https://doi.org/10.1002/j.1537-2197.1995.tb12679.x
Santos-del-Blanco L, Olsson S, Budde KB, Grivet D, González-Martínez SC, Alía R, Robledo-Arnuncio JJ (2022). On the feasibility of estimating contemporary effective population size (Ne) for genetic conservation and monitoring of forest trees. Biological Conservation 273: 109704. https://doi.org/10.1016/j.biocon.2022.109704
Scotti I, Lalagüe H, Oddou-Muratorio S, Scotti-Saintagne C, Ruiz Daniels R, Grivet D, et al. (2023) Common microgeographical selection patterns revealed in four European conifers. Molecular Ecology 32: 393-411. https://doi.org/10.1111/mec.16750
Wright S (1946) Isolation by distance under diverse systems of mating. Genetics 31: 39–59. https://doi.org/10.1093/genetics/31.1.39
Yang J, Lee SH, Goddard ME & Visscher PM (2011) GCTA: a tool for genome-wide complex trait analysis. The American Journal of Human Genetics 88: 76–82. https://www.cell.com/ajhg/pdf/S0002-9297(10)00598-7.pdf
 , 11 Mar 2024
, 11 Mar 2024Title and abstract
Does the title clearly reflect the content of the article? [ ] Yes
Does the abstract present the main findings of the study? [ ] Yes
Introduction
Are the research questions/hypotheses/predictions clearly presented? [ ] Yes
Does the introduction build on relevant research in the field? [ ] Yes
Materials and methods
Are the methods and analyses sufficiently detailed to allow replication by other researchers? [ ] I didn't check explicitly.
Are the methods and statistical analyses appropriate and well described? [ ] Yes
Results
In the case of negative results, is there a statistical power analysis (or an adequate Bayesian analysis or equivalence testing)? I don’t know (I didn't check explicitly)
Are the results described and interpreted correctly? [ ] Yes, largely.
Discussion
Have the authors appropriately emphasized the strengths and limitations of their study/theory/methods/argument? [ ] Yes
Are the conclusions adequately supported by the results (without overstating the implications of the findings)? [ ] Yes
Overall, I was satisfied with the rebuttal letter and the revisions that were done to the paper. the answers to my questions didn't always turn out they way I had hoped, but that was rather due to the sampling design and limitations of the data, not the willingness to perform additional tests.
So overall, well done!
DOI or URL of the preprint: https://doi.org/10.1101/2023.06.16.545344
Version of the preprint: 1
 , posted 20 Sep 2023, validated 21 Sep 2023
, posted 20 Sep 2023, validated 21 Sep 2023We have received three reviews on your paper. The reviewers were overall very positive, pointing out a well-motivated and well conducted study. They give suggestions for clarifications, improvements and further developments that I invite you to consider in a revised version.
I have just a few additional comment and suggestions for clarification.
On family relationships: You use two pairwise metrics, the GRM relationship coefficient, and Loiselle et al.’s 1999 kinship coefficient, to assess pairwise relatedness and its decay with distance in two sites in a Scots pine forest. Following reviewer 3, it would be interesting to see if both statistics pick up the same relationship degrees between individuals. For this, it would be useful to clarify what are the expected values and assignment ranges of each of these metrics for different degrees of relatedness. Currently, you report degrees of relatedness using the relationship coefficient but cite Manichaikul et al. 2010 who give expectations and ranges for the kinship coefficient, which can be confusing for the reader.
On the spatial extent of the observed SGS patterns: You report some differences between sites, such as relatedness in the first distance class and distance up to which individuals are more related to each other “compared to individuals in other distance classes”. It would be useful to investigate to what extent these (admittedly small) differences are biological properties, or a product of the design of distance classes and sampling range, e.g., using the same definition of classes and restricting the analysis of decay of relatedness to the same distance.
On the significance of SGS: It would be interesting to assess significance of the decay of kinship with distance using permutations for blog, so as to obtain an assessment of significance of SGS based on the decay of kinship in a single test as recommended by Vekemans and Hardy 2004; this significance test can be used to assess significance of Sp.
Carefully revise the English language please, there are some problems with missing articles and prepositions.
L.65 Unnecessarily
L.72-76 Dispersal distances are not necessarily the same in within pops (closed canopy) and for colonization (open landscapes, especially in a boreal context), perhaps to link with the discussion of dispersal distances.
L.115 What means “no minor homozygote”? Please explain more clearly the order of application of the filters; L.144-150 match the filtering mentioned briefly in L.115-116.
L.196 Spagedi doesn’t consider distance classes for blog, the regression is done over all pairwise distances between individuals.
L.199-200, please make sure subscript letters for individuals and loci are easy to distinguish and defined in the text. Currently it’s not the case.
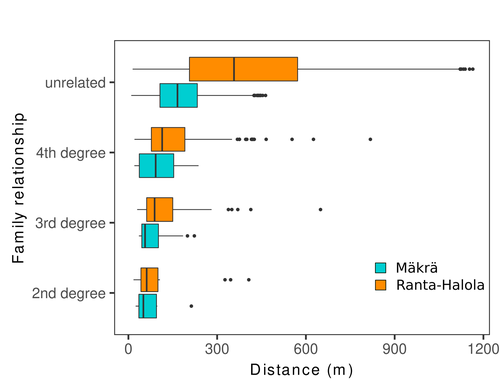
L254: What was the value of the GRM in Mäkrä in the shortest distance class, 0.004? Comparing with Fig 3, 0.0004 looks like a typo? The class with the shortest distance was not defined in the same way, making it difficult to compare GRM values.
L.256, spell “at a similar rate”, L. 258 “a negative correlation”, L. 260 “decay of relatedness with spatial distance”
L.275 Do you mean “similar” instead of “comparable” (=possible to compare)?
L.345 both values are virtually the same
L.347 not spatial structure, but spatial genetic structure. Consider using FSGS or SGS, for (fine-scale) spatial genetic structure throughout the manuscript; L.350 not population structure, but FSGS; L.356, not the spatial structure but the FSGS; verify the correct usage throughout manuscript
 , 25 Aug 2023
, 25 Aug 2023Does the seed fall far from the tree? Weak fine-scale structure in a continuous Scots pine population
This ms provides a detailed genomic insight into the population genetic structure of a conifer, and attempts to calculate the spatial extent of gene flow (pollen and seed dispersal combined), and parameters related to genetic neighborhood size.
Overall, it is a sound piece of work showing that even with wind dispersal of pollen the dispersal distance is very limited. This results in clear local genetic structure (at the level of kinship and isolation by distance), even though at the level of inbreeding coefficients the effects are very weak, yet deviating clearly from random mating.
This genetic structure and the presence of rather small neighborhoods (in terms of spatial extent) has consequences for how we calculate effective sizes in trees, even those with wind-dispersed pollen. Many methods assume that a sample used to calculate Ne or NS was taken from a randomly mating population (e.g., LD-based methods), and this paper shows that non-random mating (as a result IBD) is pervasive, even when the estimated genetic structure (F-statistics) is very weak.
A technical comment: I needed both the pdf and the html version: the pdf missed figures, the html missed formulas (embedded figures not shown). That was a bit of a nuisance.
I do have questions about parts of the methodology, especially the calculation of neighborhood size and the gene dispersal distance.
Let me start with confusion about the abbreviations used:
A. Nb is used here to denote Neighborhood Size, but Nb it is generally also used in the literature for the effective number of breeders (the effective number of parents of a single cohort in populations with overlapping generations). Nunney et al. (2016) suggest to use Nn instead of Nb for neighborhood size, to avoid this confusion. Neel et al. (2013) use NS, Wright’s Neigborhood Size. I'm using NS in my comments.
B. You calculate NS on the basis of spatial kinship decay (line 193), and from that you deduce the gene dispersal distance sigma, using the effective density De. You could actually calculate NS also genetically by means of a LD-based method. Neel et al. (2013) showed that in spatially structured populations (like this one), LDNe will estimate NS when the sample originates from an area smaller than or equal to the spatial extent of the neighborhood size (a circle with radius 2 times sigma). Since you have an idea how large Sigma is (even though you are using NS to estimate sigma), you can resample independent batches of genotypes and calculate the average NS across replicates. This would be a welcome independent estimate of NS.
C. I’m not convinced that the effective density De is a good metric to use here, and I refer to lines 205 (methods) and 290 (results). why would the mean distance between parents and offspring (=effective dispersal distance) change as a function of the Ne/Nc ratio? You sampled individuals from the Nc and observed the realized (=effective) dispersal from that same Nc, not from a theoretical equivalent Ne. Isn’t the “effective” part already accounted for when you estimated spatial kinship decay?
D. Mark that you already wrote that the median distance of the closest GRM class was 51 and 59 m, which represents dispersal rather over 2 than 1 generations (since over 1 generation GRM would be around 0.5, not 0.25). Hence these distances are 1.27 times the median (or average? unclear wording in the ms) distance across a single generation (see calculations below). As a result, the expected sigma value would be closer to 40 and 46 m.
E. All of this is under the assumption that the tree (census) density is 2000 /ha, but that would be easy to actually count and extrapolate, no? Maybe even using geospatial data?
Now, there seem to be a few very relevant things to be done with these data and results:
1. You can independently estimate Ne for the sampled area from sibship assessments (Colony), and use that to calculate Ne/Nc given that you can know Nc pretty accurately. From that result, you can check if the sigma you calculated is correct and if you should use "effective" density instead of actual density. (Mark that this sibship method is much less sensitive to spatial structure than LD-based methods, assuming that you sampled the entire area under investigation with equal intensity).
2. You can independently estimate sigma (directly from the kinship data and the spatial coordinates). See below comment pertaining to fig 5.
3. Linkage disequilibrium Ne calculations are very sensitive to the assumption of spatial genetic structure, and in continuous spatially structured populations like this one, Ne estimates will yield NS when samples are taken within a circle of radius 2sigma. Since you can resample the >400 genotypes in batches only containing individuals within the spatial extent of a Neighborhood, you can estimate NS independently of De. Once you know NS and Nc (within an area of 2PiSigma^2), you can calculate how many neighborhoods there are (and extrapolate Ne == NS*(number of neighborhoods). Or if you know the spatial extent of a Neighborhood (through the Sigma value), you can now reliably calculate the Ne/Nc ratio (actually, the NS/Nc ratio within a neighborhood, which should be the same as the overall Ne/Nc, as this is just a function of the variance in reproductive success). You can also extrapolate the Ne of the entire population: if the area occupied by the population is X, the total number of neighborhoods equals X/(4pi sigma2), and the Ne should be (X NS)/(4pi sigma2)
Minor Comments:
the authors talk about “a continuous populations”, but that requires some clarification. The Märkä population is situated on an island in a freshwater lake, for example. Although it may experience pollen flow with trees on adjacent islands or on the , it is not what I understand under the term “continuous”.
Line 29: 3210 or 3120? Differs with results section.
Line 107: the coordinates of the Mäkrä site are situated in the lake adjacent to the Mäkrä island.
Line 153: this needs better explanation. Phi-ST is generally derived from Nucleotide diversity, and adds weight to alleles that are more different from each other. How was this done in practice if you don't know the phase of haplotypes?
Line 173 - 187: Mantel tests are notoriously weak (and have a high type 2 error), and there are far better ways of addressing the question of spatial genetic structure (as noted in the MS). See Legendre & Fortin 2010 and Legendre et al. 2015. Legendre, P., and M.-J. Fortin. 2010. Why not merely use a spatial autocorrelation analysis from Moran’s I? It may not make a big difference here though.
Figure 5: could you provide sample sizes (numbers of pairwise family relationships) for the different categories? You calculated sigma indirectly by estimating NS, assuming D and assuming a certain Ne/Nc to infer De, but can’t you calculate Sigma, or even estimate a dispersal kernel function, directly from the data? Sigma is the average dispersal distance between offspring and parents, or between two offspring of the same parent. However, you have no first degree relations in your data: the smallest kinship coefficients are around 0.25 instead of 0.5. (However, half-sib relations are also just 0.25). Using information on age of trees (if you have estimates for those, e.g. from trunk diameter) you could infer which kinship combinations are parent-offspring (0.5, but absent from dataset), avuncular (0.25) and which are half-sibs (0.25). Using that information, you can estimate dispersal across two generations. Gene dispersal over 1 generation is sigma. The distance over 2 generations should (according to my deductions) be Sigma * Pi/4. (average dispersal across 1 generation from the parent will give a circle with radius sigma. Dispersal from the second generation starts on the circumference of this first circle, and a second circle is drawn. Part of the dispersal is back in the direction of the grandparent. The average distance of all points on this second circle to the origin of the first circle gives you the average distance across 2 generations. The calculation is nicely explained here https://mindyourdecisions.com/blog/2018/10/18/whats-the-average-distance-of-two-points-on-a-circle/). So across 2 generations you expect the gene dispersal distance to be 1.27 *Sigma.
Line 328: This has important implications for estimates of Ne, and how samples should be taken when estimating Ne. In effect, this spatial structure allows one to only estimate NS reliably, and then to extrapolate NS to the total area of occupation to get Ne for that population.
Line 360: Fig. 5 shows the median, not the average dispersal distance? Still, if I’m correct to deduce that this is across 2 generations instead of 1, the average dispersal distance is 54m/1.27=42 m
Line 391: Not a minor comment: IMHO, this statement very wrongly assumes that each parent produces on average just 2 offspring. Instead, each parent produces many thousands of seeds and seedlings across its lifetime, and selection acts on those seedlings, weeding out less fit genotypes. Most seedlings never reach adulthood, whereas the theoretical model assumes all reach adulthood but less fit genotypes have lower reproductive output. There is already very strong selection since orders of magnitude more offspring are produced than the number that can survive to adulthood. So I strongly question the assumption that adaptation on a very fine local scale would require extraordinary selection pressures or steep ecological gradients. Because there are so many targets of selection (=very high genotypic diversity) and because ecological space is so limited (only 1 seed per tree is expected to reach adulthood, whereas hundreds of thousands are produced across its lifetime), the response to even weak selection must be strong.
Line 397: That is just a neutral consequence of being related, no? You share large chromosomal chunks of DNA due to a shared ancestry, hence you share alleles, including rare ones.
I always sign my reports.
Joachim Mergeay, Research Institute for Nature and Forest, Belgium
In this manuscript, entitled “Does the seed fall far from the tree? - weak fine scale genetic structure in a continuous Scots pine population” Niskanen and collaborators characterize the spatial genetic structure among Scots pine individuals in two naturally regenerated sites separated by 20 km and located in a continuous South-Eastern Finnish Forest (l. 23-25). The Authors genotyped 469 adult trees from different age (33-145 years) using a custom–made Affymetrix SNP array including 407 540 markers resulting in 157 325 polymorphic SNPs (l.111-115). All the trees were georeferenced using a portable GPS locator allowing for estimation of pairwise geographical distances (l.123-130).
From this dataset, the Authors implemented different filtering steps function of the analyses (e.g. excluding related individuals, considering different MAF; details l. 133-138; 140-150; l.225-230). They conducted usual population genetics analyses to characterize population genetic structure between the two populations (FST, PCA, FST, φST), spatial genetic structure among individuals (l.157-187), estimation of related demographic parameters (Nb, sigma, Sp, l.188-223) and characterize the spread of rare alleles (l. 224-235).
Regarding the analyses of spatial structure at the individual scale:
1) they regressed the pairwise genetic distances (estimated as relatedness coefficient; GRM l.158-163) on the geographic distances and test the correlation using a Mantel test and Mantel correlogram dividing their samples in pre-defined geographic distance classes (l. 176-187).
2) They estimated Nb, sigma and Sp following Hardy & Vekemans (2004) by using a second estimator of pairwise genetic distances, the kinship estimator of Loiselle et al. (1995). Briefly, Nb, the neighborhood size, was estimated based on the regression of kinship vs. natural log of the genetic distance. Sigma, the effective dispersal, was estimated using different effective population density value and an iteration procedure while Sp, which quantifies the strength of the genetic structure among individuals, was estimated as the inverse of the regression slope divided by 1-FN (FN= mean kinship in the first distance class).
Regarding the analyses of the spread of rare alleles, the Authors focused on SNP with MAF < 0.01 and tested the regression between the GRM and the geographic distance among individuals using Mantel correlogram. They fitted the proportion of rare alleles on relatedness using local regression with sample site as fixed predictor (l. 233-235).
The Authors demonstrated a very weak genetic structure between the two sites (l.238-247). Overall, mean pairwise relatedness was low (l.253-255) but the Mantel correlogram evidenced a slight decrease of genetic relatedness with pairwise geographic distances. Interestingly, this decrease was observed at similar rate among the two sampling sites (l. 255-259). Yet, the Mantel test on the whole dataset (i.e. not considering distance classes) was significant only in one of the two populations (l.260-262). The resulting Sp were low, confirming the low spatial structure (l.262-266).
Regarding the GRM, the Authors identified 24 closely related pairs coming from the same sampling site. Decomposing the GRM in family relationships, the Authors showed the spatial aggregation of closely related individuals to be similar (same distance) in the two sites.
The estimator of dispersal (Sigma) is low.
Finally, the Authors confirmed the aggregation of related individuals also when considering rare alleles, with more related individuals sharing higher proportion of rare alleles.
The Authors discussed the spatial genetic structure among individuals in the light of non-random mating patterns previously reported (l. 324-337), highlighting their study as the first to demonstrate such structure in a large continuous population of Scott Pines.
They discussed the biological processes explaining potentially the weakness of the spatial structure focusing on long distance pollination, continuous distribution range and high population density (l. 338-343) and contrasted their results with what has been previously reported in fragmented populations of the same and other species (l.341-357).
The Authors involved the short dispersal (sigma value) estimated in their study in existing literature on wind and animal pollinated species and mentioned the limitations of the model used (i.e. Gaussian distribution of dispersal distances vs. leptokurtic dispersal kernel in wind pollinated species) (l. 368-373). Based on estimated sigma values, they inferred the strength of selection (selection coefficient) needed for their population to locally adapt. Owing to the strong coefficient of selection, they considered the likelihood for local adaptation to be low (l.374-392).
They concluded the study discussing the implications of fine scale spatial structure for the conservation and management of Scott Pine populations (l. 393-419).
Overall, this is an interesting and well written paper addressing an important issue (spatial genetic structure) in a keystone species with high economic value. The motivation of the study is well explained as well as the particular interest of the two populations (two areas within a dense continuous populations). The main objectives of the study are well exposed and references are recent and relevant in the context of the study.
The methods are relatively well explained and appropriated (but see below). The results are clear while, in my opinion, the discussion may be a bit improved.
Below I list some comments that, hopefully, will help the Authors to improve the current version of the manuscript.
#: I would expect some more details regarding demographic data. In the present form the Authors only mentioned they sampled “469 adult (33–145 years) Scots pines” l. 108. If possible, I would like to know about 1) the respective age of the two populations and 2) the size (age?) structure and 3) the density of each population. The Scott pine is the kind of species in which such data should be relatively easily estimated. In this line, I was wondering whether or not the Authors tested the evolution of the spatial genetic structure among individuals accounting for these demographic data. For instance, are the differences between the two populations in term of significance of the Mantel test and Sp (l. 260-266) potentially explained by different demographies or recolonization histories? This is probably something to discuss in the paper, particularly considering that the two populations were naturally regenerated.
The Authors also based their estimates of census density on literature (l.207-212). Does it mean it was not possible to estimate these parameters for each of the two populations directly from the field (see above?)
#: Following Rousset 2007, the regression between genetic and geographic distances in a 2D model (as it is the case in the present study) should be done considering the natural log of the geographic distance. Is there a reason to explain why the Authors used the geographic distance per se?
#: l.189-190: The definition of the neighborhood size should be rephrased according to Vekemans & Hardy 2004 (MolEcol see p.922-923) and Rousset 2008 (https://kimura.univ-montp2.fr/~rousset/hsg029_proofs_corrected.pdf; see p.14). The approximation of neighborhood size as panmictic population is not recommended.
#: Still on the neighborhood size, it is estimated in the paper from the formulae Nb=-(1-Fn)/blog. The Authors then reported two different estimates of Nb for each population considering different effective density values (l.285-287). It is not clear to me how these two De values were involved in the computation of Nb. To my understanding Nb is estimated from the slope of the linear model as supported by the formulae above (see also all the work by Rousset). Could the Authors clarify this issue?
#: Regarding the family relationships:
1) how did the Authors define the interval for each of the considered degree? In my understanding, these intervals are also impacted by the reference allele frequencies.
2) The Authors used two different estimators of genetic distance among individuals: GRM based on relatedness and Loiselle’s kinship. Do the two estimators gave the same levels of family relationship among pairs of related individuals (e.g. all the 2nd degree family relationships are found with GRM and Loiselle?)
3) It is very interesting to see that the size of the populations does not impact the mean distance among highly related individuals (Figure 5). I encourage the Authors and to emphasize this result and to improve its discussion. Is this something commonly reported in SGS studies? What is the (biologic, life strategy) hypothesis of the Authors to explain this result?
#: The discussion is likely the part that requires more rephrasing. I believe the discussion of most of the results can be improved. The same is true for the implications of the results.
1) The reasoning of the Authors is sometimes a bit hard to follow, particularly when it comes to the contrast between the restricted dispersal sigma (50m) and the weak genetic structure. Depending on the part of the discussion, it appears that there is no gene flow (e.g. l 330, 361) or that there is high gene flow through pollen dispersal (l.350-353). Beyond clarification, one way to improve the issue could be to better link the part of the discussion in which the Authors compared the Sp values among species (l.346-350) with the part of the discussion in which they compared the sigma obtained in different tree species (l. 360-368). Adding the range of geographic distances at which FST are significant in other species may also be interesting. What about the estimation of De? Is it realistic to consider values of De that will result in much higher sigma?
2) The last two paragraphs from l.402-419 are a bit too general. They introduced interesting considerations for management regarding for instance inbreeding and inbreeding depression but the Authors keep this very general perspective without linking these considerations with their own study.
3) I found the paragraph on selection (l.374-392) potentially interesting. Could the Authors be more precise regarding the known agents of selection in the Scott Pine? They computed the coefficient of selection considering a characteristic length (L) = 100m. Based on this value and their estimate of sigma they estimated that the coefficient of selection is high (at least following Authors reasoning because this value is not involved in existing published values; see below) and they mentioned that their landscape is homogenous, which limits the likelihood for strong selection. My concern here is that the reasoning may be a bit biased. Maybe the Authors should consider a characteristic length related to their homogenous landscape instead of arbitrarily choosing 100m? Or if 100m is meaningful, they should likely explain why? It would be nice also to put the value of the coefficient of selection in a broader context with example supporting the fact that 0.29 is a high value supporting strong selection.
l.386: do we really talk about the “size” of the coefficient selection? Maybe value would be better?
#: Long distance events and their implications in the observed patterns are mentioned on l. 338 and 372. In this context, I was wondering why the Authors did not try to identify these long distance events. One way would be to check for migrants (using for instance assignment tests) between the two populations? Those migrants may be proof of the long-distance events and the deviation from the Gaussian dispersal.
Minor issues:
The sentences l.111-112 and 113-115 are confusing (at least to me, sorry for that!). What is the number of genotyped SNPs? Is this number 407504 or 157325? What are the markers mentioned in l. 111-112?
From the legend (l.301-302), it seems that figures 5a and b are missing. The red line mentioned in the Figure 5 legend is not visible on the graph.
l.105: the provided link does not work.
l.334-335: What about the expected values of GRM and Loiselle kinship in case of pairs of individuals linked by selfing?
L.232: is “constructed” correct?
l.332-334: it would be nice to have estimation of selfing and survival rates.
l.353-357: not sure how to link this part on southern/northen range limits / adaptation with the rest of the paragraph. This is an interesting point, yet it deserves some more details.
l.395: what is a “lethal equivalent”?