

 based on reviews by Taom Sakal and 1 anonymous reviewer
based on reviews by Taom Sakal and 1 anonymous reviewer
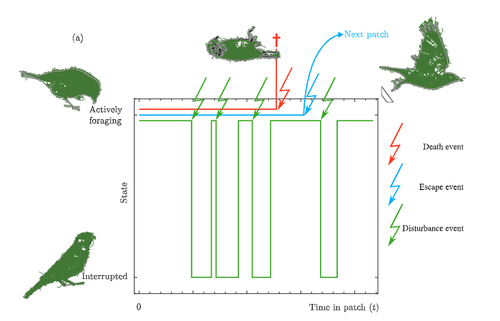
Foraging has been long been studied from an economic perspective, where the costs and benefits of foraging decisions are measured in terms of a single currency of energy which is then taken as a proxy for fitness. A mainstay foraging theory is Charnov’s Marginal Value Theorem (Charnov, 1976), or MVT, which includes a graphical interpretation and has been applied to an enormous range topics in behavioral ecology (Menezes , 2022). Empirical studies often find that animals deviate from MVT, sometimes in that they predictably stay longer than the optimal time. One explanation for this comes from state based models of behavior (Nonacs 2001)
Now Calcgano and colleagues (2024) set out to extend and unify foraging models that include various aspects of risk to the foragers, and propose using a risk MVT, or rMVT. They consider three types of risk that foragers face, disturbance, escape, and death. Disturbance represents scenarios where the forager is either physically interrupted in their foraging, or stops foraging temporarily because of the presence of a predator (i.e. a fear response). Such a disturbance can be thought of as altering the gain function for resources acquired while foraging in the patch, allowing the rMVT to be applied in a familiar way with only a reinterpretation of the gain function. In the escape scenarios, foragers are forced to leave a patch because of predator behavior, and therefore artificially decrease their foraging time as compared with their desired foraging time. Now, optimization can be calculated based on this expected time foraging, which means that in effect the forager compensates for the reduced time in the patch by modifying their view of how long they will actually forage.
Finally they consider scenarios where risk may result in death, and further divide this into two cases, one where foraging returns are instantaneously converted to fitness, and another where they are only converted in between foraging bouts. This represents an important case to consider, because the total number of foraging trips now depends on the rate of predator attack. In these scenarios, the boldness of the forager is decreased and they become more risk-averse.
The authors find that under the disturbance and escape scenarios, patch residence time can actually go up with risk. This is in effect because they are depleting the patch less per unit time, because a larger fraction of time is taken up with avoiding predators. In terms of field applications, this may differ from what is typically considered as risk, since harassment by conspecifics has the same disturbance effect as predator avoidance behaviors.
Most experiments on foraging are done in the absence of risk or signals of risk, i.e. in laboratory or otherwise controlled environments. The rMVT predictions deviate from non-risk scenarios in complex ways, in that the patch residence time may increase or decrease under risk. It is also important to note that foragers have evolved their foraging strategies in response to the risk profiles that they have historically experienced, and therefore experiments lacking risk may still show that foragers alter their behavior from the MVT predictions in a way that reflects historical levels of risk.
References
Calcagno, V., Grognard, F., Hamelin, F.M. and Mailleret, L. (2024). Taking fear back into the Marginal Value Theorem: the risk-MVT and optimal boldness. bioRxiv, 2023.10.31.564970, ver. 3 peer-reviewed and recommended by PCI Evolutionary Biology. https://doi.org/10.1101/2023.10.31.564970
Charnov E. (1976). Optimal foraging the marginal value theorem. Theor Popul Biol. 9, 129–136.
Menezes, JFS (2022).The marginal value theorem as a special case of the ideal free distribution. Ecological Modelling 468:109933. https://doi.org/10.1016/j.ecolmodel.2022.109933
Nonacs, P. 2001. State dependent behavior and the Marginal Value Theorem. Behavioral Ecology 12(1) 71–83. https://doi.org/10.1093/oxfordjournals.beheco.a000381
DOI or URL of the preprint: https://doi.org/10.1101/2023.10.31.564970
Version of the preprint: 2
 , posted 19 Apr 2024, validated 22 Apr 2024
, posted 19 Apr 2024, validated 22 Apr 2024Dear Authors,
Thanks for your revisions and for your detailed responses to the comments. The changes have addressed almost all of the prior queries, and I would like to recommend this article for PCI, and I still have a request for changes to the section on Disturbance Scenarios. I apologize for the delay, it was partly due to needing to take the time to work out the questions I had about your formulation and response to the prior reviews.
My main question is the similar to one I posed in the original review, but I think I can express it more clearly now. A foraging animal could keep track of total time foraging in a patch, and have a leaving rule that is to leave at a constant time within the patch. This is the formulation that you have adopted. You point out that the average gains for spending t time units in a patch depend on the actual time spent foraging (which is lower than time in the patch) and the variance in time spent foraging (because the gain curve has negative second derivative). There may also be a direct cost of disturbance, which you include in eq 2.
An alternative assumption about forager behavior is that they may be able to track how much time they spend actually foraging in the patch. In other words, they could track t_f, time foraging in the patch, t_v, time being vigilant in the patch, and then t=t_f+t_v is total time in the patch. They could have a rule to leave at a specific t_f. This gives a average return function of
f[t_f] / (T + t)
Taking the derivative with respect to t_f and solving for it being 0 gives
f’[t_f] = (beta + gamma) f[t_f] / (T gamma + t_f (beta + gamma)
I believe that this solution will have higher average fitness than the rule of leaving after a fixed total amount of time in the patch since it allows the animal to use more information. I believe that it would be valuable to relate the “fixed total time in patch” rule to a “fixed foraging time in patch” rule, even if only to say these are alternative assumptions about how forager decisions could be made.
Fundamentally, I think it is important to note what assumptions go into the version presented in the paper. The presentation around eq 2 does not explain verbally how the equation was derived, although you do a great job of explaining what the terms in eq 2 represent. Before presenting eq 2 you should explain that the assumption is that the animal can only track total time in the patch. As you explained in your response letter, it cannot directly assess the current patch quality.
DOI or URL of the preprint: https://doi.org/10.1101/2023.10.31.564970
Version of the preprint: 1
 , posted 15 Jan 2024, validated 16 Jan 2024
, posted 15 Jan 2024, validated 16 Jan 2024Dear Authors,
The article that you requested be evaluated has been read and commented on by two reviewers and myself. All the readers found the subject interesting and the potential contributions interesting. There are several areas where readers asked for more detail and clarification, and questioned whether all of the technical details had been properly considered. One reader also felt that the overlap with existing publications was high, and that the authors needed to explain more clearly how this current work fits into the broader literature.
I was very interested to read this article and found the introduction very helpful for getting an idea of where the article was going and of summarizing existing work in the field. I have a few speciifc queries of my own related to the derivations and results:
1) the use of the phrase "transformation" and of "newtonian" time seem unecerssarily confusing. The functions presented are expected gains or expected amounts of time spent. There is no actual transformation of time. I would simply call these functions expected gain and expected amount of time spent in patch.
2) The article focuses on calculating expected gain as a function of the strategy, and the strategy is the amount of time spent in the patch. I don't see derivations in the article for the optimality of the strategies. In particular, equation 2 defines a function Fhat(t) that represents the mean energy gain for departing after t time units. While this equation makes perfect sense to use when calculating the average gain per time one gets when leaving a patch, it actually does not represent the current gains within a patch. If a focal animal has not been disturbed and reaches t*, it will have a different level of gain than the derivative of the expected value of gain. I do not see an explanation in the article for how using the derivative of expected gain gives the optimal solution. It seems to me that a strategy that leaves when the current gain drops to the expected average gain is optimal, but this does not results in a strategy of leaving at a constant time.
3) After equation 3, it seems that the describerd scenario involves an animal loosing time if it is disturbed. But it can just start foraging in another patch, it doesn't loose the time. This is only revealed much later in the paper.
I beleive there is a critical piece missing from this article and that you need to show how the strategy of leaving when the expected gains per time drop to the global expected gains per time. Other than that, the main recomendaitons involve altering how you talk about transformations and non-newtonian time and some better integration of existing literature.
 , 31 Dec 2023
, 31 Dec 2023