Foraging has been long been studied from an economic perspective, where the costs and benefits of foraging decisions are measured in terms of a single currency of energy which is then taken as a proxy for fitness. A mainstay foraging theory is Charnov’s Marginal Value Theorem (Charnov, 1976), or MVT, which includes a graphical interpretation and has been applied to an enormous range topics in behavioral ecology (Menezes , 2022). Empirical studies often find that animals deviate from MVT, sometimes in that they predictably stay longer than the optimal time. One explanation for this comes from state based models of behavior (Nonacs 2001)

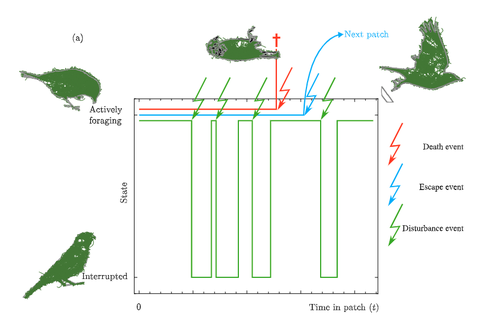
Now Calcgano and colleagues (2024) set out to extend and unify foraging models that include various aspects of risk to the foragers, and propose using a  risk MVT, or rMVT. They consider three types of risk that foragers face, disturbance, escape, and death. Disturbance represents scenarios where the forager is either physically interrupted in their foraging, or stops foraging temporarily because of the presence of a predator (i.e. a fear response). Such a disturbance can be thought of as altering the gain function for resources acquired while foraging in the patch, allowing the rMVT to be applied in a familiar way with only a reinterpretation of the gain function.  In the escape scenarios, foragers are forced to leave a patch because of predator behavior, and therefore artificially decrease their foraging time as compared with their desired foraging time. Now, optimization can be calculated based on this expected time foraging, which means that in effect the forager compensates for the reduced time in the patch by modifying their view of how long they will actually forage.

Finally they consider scenarios where risk may result in death, and further divide this into two cases, one where foraging returns are instantaneously converted to fitness, and another where they are only converted in between foraging bouts. This represents an important case to consider, because the total number of foraging trips now depends on the rate of predator attack. In these scenarios, the boldness of the forager is decreased and they become more risk-averse.

The authors find that under the disturbance and escape scenarios, patch residence time can actually go up with risk. This is in effect because they are depleting the patch less per unit time, because a larger fraction of time is taken up with avoiding predators. In terms of field applications, this may differ from what is typically considered as risk, since harassment by conspecifics has the same disturbance effect as predator avoidance behaviors.

Most experiments on foraging are done in the absence of risk or signals of risk, i.e. in laboratory or otherwise controlled environments. The rMVT predictions deviate from non-risk scenarios in complex ways, in that the patch residence time may increase or decrease under risk. It is also important to note that foragers have evolved their foraging strategies in response to the risk profiles that they have historically experienced, and therefore experiments lacking risk may still show that foragers alter their behavior from the MVT predictions in a way that reflects historical levels of risk.

References

Calcagno, V.,  Grognard, F., Hamelin, F.M. and  Mailleret, L. (2024). Taking fear back into the Marginal Value Theorem: the risk-MVT and optimal boldness. bioRxiv, 2023.10.31.564970, ver. 3 peer-reviewed and recommended by PCI Evolutionary Biology.  https://doi.org/10.1101/2023.10.31.564970

Charnov E. (1976). Optimal foraging the marginal value theorem. Theor Popul Biol. 9, 129–136.

Menezes, JFS (2022).The marginal value theorem as a special case of the ideal free distribution. Ecological Modelling 468:109933. https://doi.org/10.1016/j.ecolmodel.2022.109933

Nonacs, P. 2001.  State dependent behavior and the Marginal Value Theorem. Behavioral Ecology 12(1) 71–83. https://doi.org/10.1093/oxfordjournals.beheco.a000381