All you ever wanted to know about Ne in one handy place

Dear Recommender

Please find below the rebuttal regarding our preprint submission PCIEvolBiol #651

We have implemented all requested additional elements, except for the one "line 126" that we failed to insert, because we did not understand where to insert "from the pool". There was some discrepancies with the line numbering in Dr Taylor's review and our version of the preprint, but we believe we managed to find the correspondences.

We hope that our preprint is now suitable for recommendation in PCI Evol Biol and remain at your disposal for any modification you might find necessary

Sincerely

Thierry de Meeûs

 

Second review of de Meeus and Nous (2023): A new and almost perfectly accurate
approximation of the eigenvalue effective population size of dioecious populations: comparisons with former other estimates and detailed proofs.

 

The authors have extensively revised their manuscript and have at least acknowledged and discussed all of the major questions that I raised concerning the original submission. My overall assessment of the work has not changed very much. I agree with the authors that there is intrinsic value in having more accurate approximations for theoretical quantities such as the eigenvalue effective population size of a dioecious population. It is also useful to have explicit derivations for these other approximations, especially when these are accompanied by biological interpretations for the different terms that appear in these expressions. At the same time, I suspect that the relatively small differences between these various approximations will be swamped by the errors arising from using models that ignore demographic complexities such as population dynamics, population structure and complex life histories. I also remain somewhat skeptical of the value of methods-of-moments estimators for Ne, particularly when these require the exclusion of otherwise informative data. I understand that implementing Bayesian and likelihood-based estimators is non-trivial, but these approaches are more statistically sound and should make more efficient use of all of the available data.

 

Since it would require extensive work, far beyond the scope of the current manuscript, to fully address either of these criticisms, I am satisfied with the additional text included by the authors discussing the limitations of their work. There is much more to be said about the relationship between genetic drift and demographic processes, but this manuscript does make some useful and interesting contributions. See below for a list of suggested grammatical and textual corrections.

 

Jay Taylor (9 May 2023)

 

Authors: We are grateful for Dr Taylor's comprehension and extensive work to improve our manuscript. We have implemented all suggested revisions asked (except "line 126") (see below) and hope the preprint is now suitable for recommendation.

 

Minor corrections:

line 2:“population size of a dioecious population: comparisons with other estimates and detailed proofs”

 

Authors: done

 

 

line 23: “the eigenvalue effective population size of a dioecious population”

 

Authors: done

 

 

line 26: “provides more accurate results in very small populations”

 

Authors: done

 

 

lines 37-45: I would be careful to distinguish between the Castle-Weinberg model and the Fisher-Wright model: the latter includes the assumption of binomial sampling in a finite population, whereas the former assumes an infinite population where genetic drift can be neglected. In my opinion, it is binomial sampling that is the core assumption of the Wright-Fisher model and it is in terms of this particular probabilistic model for parent-offspring relationships that the various concepts of effective population size are defined.

 

Authors: We have added some comments dealing with Dr Taylor's concerns.

 

 

line 63: “In this note, we review some of these results and we then derive a new and apparently more accurate approximation for the eigenvalue effective population size of a dioecious population.”

 

Authors: done

 

 

 line 70: “can easily access this knowledge.”

 

Authors: done

 

 

line 126: “from the pool”

 

Authors: Here we are sorry but we did not find were to put this adding.

 

line 128: “the probabilities of identity”

 

Authors: done

 

 

line 265: “In Figure 1”

 

Authors: Done but it was found in line 253. We hope this was the right one.

 

 

Figure 1: Please specify the actual sex ratio(s) used to obtain the results shown in the figure on the left (uneven sex ratio).

 

Authors: It appeared very difficult to figure the different sex ratios corresponding to Figure 1 (almost all possible values from 1/99 to 5/11). Instead, we have added the equation giving the threshold value for the sex ratio (SR2=3-2sqrt(2)) that makes Balloux's equation above or below Equation 13. If we change the abscissa with SR values, then Figure 1 becomes very confusing. Nevertheless, with SR2, it is easy to evaluate what values SR takes in Figure 1, as now explained in the amended version of the manuscript.

 

 

line 329: “Notice that equation 20 differs from equation 4 by the subtraction of half an individual.” 

 

Authors: Done (but in line 313)

 

 

line 372: “where only dioecy”

 

Authors: Done (but in line 350)

 

 

line 373: “2) to present detailed derivations of both the old and new results that would be accessible to most readers”

 

Authors: Done (but in line 351)

 

 

line 384: “with not much harm”

 

Authors: Done (but in line 362)

 

 

line 472: “We may also bear in mind that although random mating was assumed, we did not specify any reproductive strategy” 

 

Authors: Done (but in line 444).

 

 

line 495: “FIS should be estimated from adults”

 

Authors: Done (but in line 466).

 

 

General formatting suggestion: New lines should only be indented if they appear at the beginning of a new paragraph and not simply because they are preceded by an equation. Otherwise, the text becomes fragmented into numerous paragraphs containing only one to two sentences apiece (plus an equation), which reduces the coherence of the writing. It is perfectly acceptable for one or more equations to appear within a paragraph, provided the surrounding text addresses one or a few closely related ideas.

 

Authors: Done

Rebuttal letter

 

Dear Recommender

We have taken into account all remarks and suggestions of both referees and amended our manuscript accordingly. The input from Dr Taylor was very significant,. This explains the time it took for us to follow all his suggestions. We believe that the modifications that followed considerably improved the quality of ourpaper.

You will find below all referees' remarks and our answers

We hope thatyou will find that our preprint is now suitable for recommendation and remain at your disposal for any modification that you may find necessary.

Sincerely

Thierry de Meeûs

 

 

Round #1

by Charles Baer, 31 Mar 2023 14:42

Manuscript: https://doi.org/10.5281/zenodo.7665497 version 4

A new and almost perfectly accurate approximation of the effective population size of dioecious populations: comparisons with former estimates and detailed proofs

 

Dear Dr. de Meeus,

 

I have now received two expert reviews of your article "A new and almost perfectly accurate approximation of the effective population size of dioecious populations: comparisons with former estimates and detailed proofs".  As you will see, both reviewers find the work meritorious in principle.  One reviewer (Jay Taylor) makes numerous substantive suggestions, none of which I especially disagree with.  Accordingly, I think your submission warrants revision.  Please address all of the reviewers' comments in the revised version.

 

Sincerely,

 

-Charles Baer​

 

Reviews

Reviewed by Jesse ("Jay") Taylor, 31 Mar 2023 02:58

Review downloaded and copied-pasted below with our answers

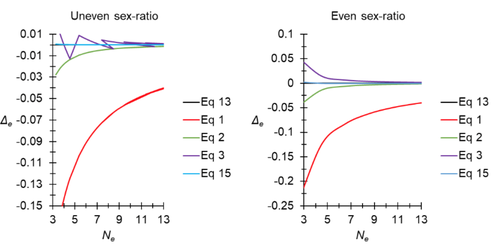
Review of de Meeus and Nous (2023): A new and almost perfectly accurate approximation of the effective population size of dioecious populations: comparisons with former estimates and detailed proofs. This manuscript makes three contributions to the theoretical population genetics of dioecious populations. First, the authors derive several novel expressions for the eigenvalue effective population size of a randomly-mating population conforming to a two-sex version of the Wright-Fisher model. They begin by deriving a system of recurrence equations for the probability of identity-by-descent between pairs of alleles taken either from a single randomly sampled individual or from two distinct randomly sampled individuals. They then show that the equilibrium effective population size can be calculated from the leading eigenvalue of this recurrence, which allows them to derive an exact expression for Ne in terms of the numbers of females Nf and males Nm (their equation 13). They also give a somewhat simpler but very accurate approximation for Ne (their equation 15). Both the exact result and its approximation are compared with several alternative expressions for the eigenvalue effective population size of a dioecious population and shown to be more accurate, especially at very low population sizes (Figure 1). Secondly, the authors use these results to formulate two novel estimators of Ne based on Wright's FIS (equations (19) and (21)) and they show that these outperform several existing FIS-based estimators of Ne when FIS is equal to its expected value (Figure 2). On the other hand, when FIS is estimated from sequence data (as would usually be the case), simulations suggest that all of the various estimators of Ne considered in this paper are significantly biased. The third contribution comes in the form of an extended series of appendices in which the authors provide detailed derivations of a number of expressions for the inbreeding, eigenvalue and coalescent effective population sizes that have been suggested by other researchers, sometimes without explicit derivation.

All three of these contributions have some value. In particular, one strength of the manuscript is that the authors provide detailed, step-by-step derivations of all of the main results, both new and old, making it easier for the reader to follow the assumptions and algebra leading to the various equations that appear in the text. Nonetheless, I found some of the authors' claims about effective population size unclear or questionable. These and other concerns and suggestions are discussed below.

(1) The most pressing question that I have concerns the scope and robustness of the authors' main results. Genetic drift can be influenced by several factors, including (a) the reproductive system, (b) within-generation reproductive variance, (c) life history (e.g., overlapping vs. non-overlapping generations; iteroparity vs. semelparity), (d) demographic history (e.g., changes in population size and/or sex ratio), (e) population structure, and (f) selection at linked sites (background selection and selective sweeps). This paper focuses on the impact of dioecy and sex ratio on genetic drift but it largely ignores all of the other factors mentioned above, leaving me wondering about the biological relevance and validity of the authors' results, especially equations (13), (15), (19) and (21). Are there any real populations that closely conform to the two-sex Wright-Fisher model used to derive these results and, if not, what are we actually estimating if we apply equations (19) and (21) to genetic data?

To be specific, I would be interested in seeing how the results given in these four equations are affected by the following complications. First, how do these expressions change if the within-generation reproductive variance (which could differ between males and females) differs from that obtained under the multinomial sampling assumed by the Wright-Fisher model? The authors do refer to the possibility of defining effective numbers of breeders, but it isn't obvious to me that their results on the eigenvalue effective population size will remain valid if Nf and Nm are simply replaced by effective numbers of female and male breeders, especially if male and female reproductive success are correlated. Perhaps a dioecious version of the exchangeable Cannings model could be used to investigate this complication? A second complication that I think merits attention is the impact of population size and sex ratio fluctuations on these results. The authors observe that the discrepancies between their expressions for the eigenvalue effective population size and those obtained by earlier authors are proportionately greatest when the population size is small. However, small populations are also probably more strongly affected by demographic stochasticity, which can lead to proportionately larger fluctuations both in total population size and in sex ratio. The expressions given in equations (13) - (21) were derived by assuming that the population is at equilibrium (in some sense), which likely requires a time average over multiple generations, during which the numbers of adult females and males may fluctuate. How will this impact the formulas given in equation (13) and (15), and do the estimators derived in equations (19) and (21) remain valid if Nf and Nm are replaced by their harmonic means or some other appropriate averages? Alternatively, is it possible to derive comparable results for the single generation eigenvalue effective population size (which can then fluctuate across generations) without insisting on equilibrium? (For example, we can define a time-dependent coalescent effective population size in terms of the instantaneous pairwise coalescent rate, which can then be estimated using Bayesian skyline estimators.). If it isn't possible to perform additional theoretical or simulation-based studies of these complications within the scope of the current manuscript, then I think that the authors should at least acknowledge that the scope and applicability of their results may be limited in practice.

 

Authors answer: 

We thank Dr Taylor for these extensive comments and accurate questions. The complications he is suggesting are far beyond our mathematical skills, and in particular our ability to make the algebraic adjustments needed understandable to most readers, which was one of the main goals of our paper. It is also not in the scope of our manuscript. We have thus added a full paragraph discussing such issues and the resulting limitations that this may have on field applications. We hope that this paragraph will meet Dr Taylor's satisfaction.

 

 

(2) As the authors acknowledge in their introduction, there are several formal definitions of effective population size which do not coincide in general and so it is somewhat misleading to speak of the effective population size without specifying which concept is in use. Although it may be acceptable to use the wording 'the effective population size' where the concept is clear by context, I think that this language should be avoided otherwise. For this reason, I would encourage the authors to change the wording of the title and the abstract so that they explicitly refer to the eigenvalue effective population size that is the main focus of this manuscript.

 

Authors answer:

Dr Taylor is right and we amended the title and the abstract accordingly.

 

 

(3) I would encourage the authors to include a more detailed and explicit description of each of the models being studied in the paper. For example, I think that the subsection titled 'The general model of a dioecious pangamic population' should begin with a detailed description of the model that is used to derive equations (7) and (8). This would include the fact that (i) we are considering a diploid locus; (ii) that the numbers of adult females and adult males participating in reproduction is constant from generation to generation; (iii) that the genotype of each individual alive in generation t + 1 is determined by independently sampling a single allele uniformly at random and with replacement from the Nf adult females alive in generation t and then doing the same from the Nm males alive in generation t; (iv) that the maternal and paternal alleles are sampled independently, etc. I think that detailed, explicit descriptions of the biological models used to derive the theoretical results given in the paper are at least as important as the detailed, explicit descriptions that the authors give of the algebraic transformations that they apply to these results. 

 

Authors answer: 

Dr Taylor is right. We have added a few lines to complete the description of the model and hope that Dr Taylor will agree with these explanations.

 

 

(4) The authors note that their estimates of Ne are negative and therefore not biologically meaningful whenever FIS is estimated to be positive. To address this problem, they recommend excluding loci at which FIS is estimated to be positive when estimating Ne. This strikes me as ad hoc and statistically unsound. Perhaps a better approach would be to estimate Ne directly from the observed and expected heterozygosities using either maximum likelihood or Bayesian estimation. For example, for the small populations that seem to be most relevant to the concerns of this manuscript, it may not be too computationally challenging to use either approximate Bayesian computation or MCMC to estimate the posterior distribution of (Ne;Nm) (and any nuisance parameters such as mutation rates). One could then easily estimate the posterior distribution of Ne using equation (13). What is the value of introducing yet another statistically questionable method-of-moments type estimator when one can perform maximum likelihood or Bayesian analysis? 

 

Authors answer: 

Here we are sorry to be unable to follow Dr Taylor's suggestions. First, we do not see why it is unsound not to consider loci with FIS≥0 since infinity, or negative values (which sounds inappropriate to us), to which such values would correspond to, cannot be used to compute any averaged value. We moreover hardly see how expected (He) and observed (Ho) heterozygosities would change anything to this problem, since for such loci He≥Ho. Bayesian or MCMC estimate are not in the scope of our paper, and we frankly would not know how to implement those. We sincerely believe that, if it was so easy to implement, such methods would already be available and popular. We also think that the question asked about " the value of introducing yet another statistically questionable method" does not appear very fair to us.Indeed, it was not us who introduced and popularized such an approach. This was done by respectable colleagues who published such results in the most prestigious journals in the field, and where, as it seems, no referee or editor asked them such a question. Testing the validity and usefulness of this approach, as discussed at the end of our manuscript, will require extensive simulation-based analyses, which, again, are not in the scope of our paper. We have now more clearly defined the scope of our article in the second paragraph of the discussion section. We sincerely hope that this will be enough to convince most readers.

 

 

(5) It might be useful to mention that the FIS-values used to estimate Ne should be estimated in reproductively mature individuals. In small populations these statistics could fluctuate significantly within generations due to random survival from birth to reproductive maturity.

 

Authors answer: We have added a paragraph on this issue in the amended manuscript.

 

 

(6) The equations presented in lines 1185-1211 in Appendix 6 are not quite correct. In particular, beginning on line 1185, there is a series of identities which contain an infinite series on the left-hand side and a finite series (also over t) on the right-hand side. To fix this, you need to take limits  on the right-hand side. Provided that all of the eigenvalues have modulus less than 1, these limits will exist and be finite. Alternatively, the desired result can be derived as follows. 

 

Authors answer:

Here we did not copy-paste Dr Taylor's equations as these produced very odd things in this word document. We thank Dr Taylor for this precision. We fixed this issue by replacing the "infinite" sign by n, and computed the average coalescent time at generation n. This allowed us to keep all terms until the very last equation, so that we can see what need to be neglected, e.g. when n is very big (e.g. infinite).

 

 

Minor corrections:

line 55:"Many species have separate sexes. Several authors have investigated the impact that dioecy and sex ratio have on effective population size."

 

Authors answer:

Done

 

 

line 58: "leads to an approximation that appears closer"

 

Authors answer:

Done

 

 

line 60: "We also propose another estimator of"

 

Authors answer:

Done

 

 

line 68: "The effective population size of a dioecious population has been defined in different ways."

 

Authors answer:

Done

 

 

line 75: "for the eigenvalue effective population size Ne"

 

Authors answer:

Done

 

 

line 86: "Another consequence is that"

 

Authors answer:

Done

 

 

line 99: No comma is required after Balloux (2004)

 

Authors answer:

Done

 

 

line 121: Why is it necessary to assume that the number of matings is very large?

 

Authors answer:

We have added " This way, the probability of mating between two individuals remains independent of previous copulas these may have been involved in"; Though we know that this may not be very relevant here, since monogamy gave identical results as those with random mating with even sex-ratio.

 

 

line 235: "The reasons for this discrepancy between these two sets of equations are unclear due to the lack of details in Balloux' paper."

 

Authors answer:

Done

 

 

line 245: "This bias is very small when Ne > 10."

 

Authors answer:

Done

 

 

Figure 1: Please specify the actual sex ratio(s) used to obtain the results shown in the Figure on the left (uneven sex ratio). Also, why does purple curve have such a jagged appearance in this Figure and why, in particular, does it appear to jump back and forth when Ne > 7?

 

Authors answer: We apologize for not explaining it better in previous versions. In the new Appendix 9, we now give the analytical solution for this and give the result in the text: Balloux's equation will provide an over-estimate when SR>SR2, an under-estimate when SR<SR2 and will be exact when SR=SR2=3-2 . After that, from Figure 1, it can be seen that the bias oscillates as Ne increases and SR changes, and that the amplitude of oscillations decreases.

 

 

line 309: What does very big mean in this setting? Ne > 20? Ne > 100?

 

Authors answer:

The sentence was changed in order to avoid such subjective statements.

 

 

line 311: "in the opposite direction"

 

Authors answer:

Done

 

 

Figure 2 legend: add a space before the equation numbers, e.g., Eq 5.

 

Authors answer:

Done

 

 

line 380: "It is worth recalling that the FIS-based estimate given in Equation (21) assumes an even sex ratio."

 

Authors answer:

Done

 

line 396: "large variances"

 

Authors answer:

Done

 

 

line 397: "will have a large impact on FIS-based estimates of Ne.

 

Authors answer:

Done

 

 

line 408: "In addition to the fact that it is generally preferable to work with the most accurate equation, these results are likely to be especially pertinent for certain types of biological systems that are able to persist for extended periods despite having very small effective population sizes."

 

Authors answer:

Done

 

 

line 414: "a female enters a brood cell, which she caps, where she feeds on the bee larva and then gives birth to a haploid male, which later mates with its"

 

Authors answer:

Done

 

 

line 422: "may not be rare in dioecious parasitic"

 

Authors answer:

Done

 

 

line 439: "different kinds of loci"

 

Authors answer:

Done

 

 

line 453: "were positive and therefore could not be used to estimate Ne."

 

Authors answer:

Done

 

 

line 480: "Simulation studies could be used to identify an estimator that more accurately approximates the eigenvalue effective population size of genotyped populations." As discussed above, I would argue that there is no such thing as the 'real effective population size'.

 

Authors answer:

Done

 

 

line 487: "may lead to underestimates."

 

Authors answer:

Done

 

 

line 493: I don't know what you mean by "important" population sizes.

 

Authors answer:

We have added more information about this.

 

 

line 721: "To compute the inverse of a 3x3 matrix"

 

Authors answer:

Done

 

 

line 788: "an infinite collection of eigenvalue that all satisfy"

 

Authors answer:

Done (with "eigenvectors")

 

 

line 802: "Computing matrix powers is difficult except for diagonal matrices."

 

Authors answer:

Done

 

 

line 843: "Consequently, we can use equation (A3-3) to calculate the power of any diagonalizable square matrix."

 

Authors answer:

Done

 

 

line 845: "We can now derive some other properties of eigenvalue-eigenvector pairs (eigenpairs)."

 

Authors answer:

Done

 

 

line 874: You should remark that equation (A3-6) only applies when S is invertible.

 

Authors answer:

Done

 

 

line 971: Castle-Weinberg (capitalization)

 

Authors answer:

Done

 

 

Appendix 5: Perhaps it would be clearer to write Hdi and Hmon in place of Hobs and Hexp. To me, the notation Hobs and Hexp suggests that we are working with the observed and the expected heterozygosity, which is not the case here. Instead, Hobs is the expected heterozygosity in a dioecious population, while Hexp is the expected heterozygosity in a monoecious population.

 

Authors answer:

Done

 

 

line 1024: "The variance of a difference between two uncorrelated (e.g., independent) random variables"

 

Authors answer:

Done

 

 

line 1099: "the probabilities that the same allele is sampled twice, either in one individual or in two distinct individuals from the same population. Let u be the mutation rate per generation." 

 

Authors answer:

Done

 

 

line 1100: Do equations (A6-1) assume the infinite allele model?

 

Authors answer:

Yes, and we now precise this.

 

 

Equation (A6-3): There is an extra 1 in the expression shown in A2;2.

 

Authors answer:

Deleted

 

 

line 1131: "the second term in these equations will increase with t, albeit at a diminishing rate, while the first term will decrease with t."

 

Authors answer:

Done

 

 

line 1153: "the probability of pairwise coalescence"

 

Authors answer:

Done

 

 

line 156: To be consistent you should capitalize the entries in the vector shown in (A6-8).

 

Authors answer:

Done

 

 

lines 1158-1160: Please clarify what you mean by the coalescent probabilities here. In most scenarios commonly considered in biology, the probability that two lineages will eventually coalesce in the past is 1.

 

Authors answer:

We took this from Rousset's book. This is an event of coalescence somewhere in the past. We have added "somewhere" in the sentence to make it clearer.

 

 

line 1181: Since A is a 2x2 matrix, shouldn't i be restricted to the values 1 and 2?

 

Authors answer:

Yes, Dr Taylor is right. This was given for the general case. We have added a comment to make it clearer.

 

 

line 1368: This identity (the chain rule) is incorrect as written. It should be replaced by the expression (f _ g)0(x) = f0(g(x))g0(x).

 

Authors answer:

Done

 

 

line 1372: Replace derivable by the word differentiable.

 

Authors answer:

Done

 

 

line 1461: "Assuming that u<<1"

 

Authors answer:

We have preferred "Taking into account", because mutation rate is always a very small probability.

 

 

line 1468: I disagree that the effective number of breeders is in general equal to the exact number of reproducing adults. As discussed above, we need to account for within-generation variance in reproductive success which depends not only on the number of adults that reproduce but also on the number of offspring that survive to adulthood.

 

Authors answer:

We have changed it into "of adult parents of the individuals in the population"

 

 

line 1493: "At equilibrium, the vector of genetic identities satisfies the equation"

 

Authors answer:

Done

.

 

lines 1509-1525: I think that this paragraph needs to be reworded, e.g., "The recursion for the identity between individuals can be determined by conditioning on the ancestry of the sampled pair in the previous generation. One possibility is that the two sampled individuals are sibs, i.e., they share the same parents, which is true with probability 1/(N/2). In this case, with probability 1/2, the two alleles will have come from the same parent, in which case they are equally likely to be derived from a single parental allele or from both parental alleles. In the former case, the sampled alleles are necessarily IBD, whereas in the latter case, the probability that they are IBD is QI(t-1). Alternatively, with probability 1/2, each sampled allele may have come from a different parent, in which case the probability that they are IBD is QS(t-1). The second possibility, which has probability 1 - 1/(N/2), is that the two sampled individuals are not sibs, in which case the probability that the sampled alleles are IBD is QS(t-1).

 

Authors answer:

Done

 

 

 

Reviewed by anonymous reviewer, 08 Mar 2023 16:53

 

I reviewed for the third time the paper newly entitled “A new and almost perfectly accurate approximation of the effective population size of dioecious populations: comparisons with former estimates and detailed proofs”

 

In this new version the authors replied to previous remarks and criticism from the editor and reviewers. Notably, the authors added some details where needed, gave more details about the assumptions made in the model, and gave more details about the utility of the new estimator proposed.

 

Table 1 of the previous version has been replaced by Figure 1 of the current version, improving a little bit the understanding and the visualization of how and when the different equations presented in the note approximate correctly or not the true effective population size. 

 

General comment:

 

As I mentioned in the previous reviews, the paper is generally well-written, and is more accessible to a broad audience with the new changes requested by R3 and the previous recommender Dr. Heuertz. The mathematics behind the model seems correct. But, again, and as mentioned in the previous reviews, if the new approximation is slightly better than others to estimate extremely small population sizes, it is notable that other approximations were not that bad (eqs. 2 & 3 have a maximum 5% of deviation from eq. 1), and the “superiority” of eq. 15 is limited to N_E ranging from 3 to 13 individuals, depending on if the sex ratio is even or not. The authors have nevertheless added a section in the discussion justifying in which situations their approach should be useful, notably for dioecious parasitic organisms. 

 

Authors' answer: 

 

We thank the referee for these positive comments

 

 

Minor comments:

 

Lines 32-54: The introduction is generally lacking references around the key terms and statements described, and that have been described elsewhere before.

 

Authors'answer: 

We have now added several references. I hope we found enough of those and that this will meet the referee's satisfaction.

 

 

Line 55: “paid interest in” -> “paid attention to”?

 

Authors' answer: 

The sentence was changed by Dr Taylor

 

 

Line 83: In the PDF version it is hard to read if N_M is subtracted from or multiplied by N_F.

Authors' answer: 

Yes, the referee is right, we replaced this by an equation with the equation editor of word and it looks much clearer now.

 

 

Line 224: “members” -> “brackets” or “parentheses”?

 

Authors answer: 

OK, this obviously was not clear. Here, we meant "expressions  that are squared" or "terms that are squared". We chose "terms" and hope it is clearer now.

 

 

Line 241-243: Well, eq.1 strongly underestimates Ne for a limited set of values. When Ne equals 7, the error around delta_e is below 10%.

 

Authors' answer: 

The referee is right, we have added ", as compared to other approximations" at the end of this sentence.

 

 

Line 243-245: “Similar amplitude” is a bit misleading, as the error of equations 2 and 3 is very low (maximum 5%).

 

Authors' answer: 

We agree and changed this part into " seem to display an equivalently small bias"

 

 

Line 307-309: Again “substantially” seems a bit strong here, as well as “very big Ne”, because a small Ne of 10 leads to only 5% errors.

 

Authors' answer:  

This was changed into " tend to over-estimate Ne as compared to other estimates, unless population size becomes big enough.

 

 

Line 312: Same remark, “substantial” seems inappropriate here.

 

Authors' answer: We changed this into " is only visible"

 

 

 Line 357: Again, “substantial” seems inappropriate here.

 

Authors' answer:

We tried to improve this sentence by replacing this by " To be as accurate as Equation 21, Equation 2 indeed requires Ne > 10"

 

 

Line 366: Equation 5 of the present manuscript.

 

Authors answer: done

 

 

Line 399-401: The sentence is very confusing here. In addition, “under-estimates” -> underestimation?

 

Authors answer: 

All terms "over-estimates and "under-estimates" were amended accordingly in this paragraph