
BAER Charles
- https://people.clas.ufl.edu/cbaer/, University of Florida, Gainesville, United States of America
- Experimental Evolution, Population Genetics / Genomics, Quantitative Genetics
- recommender
Recommendations: 3
Reviews: 0
Recommendations: 3
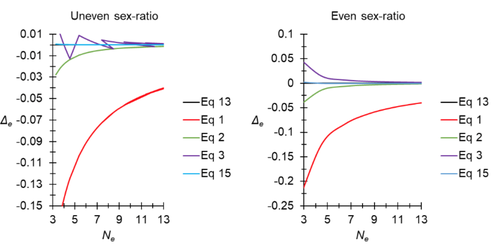
A new and almost perfectly accurate approximation of the eigenvalue effective population size of a dioecious population: comparisons with other estimates and detailed proofs
All you ever wanted to know about Ne in one handy place
Recommended by Charles Baer based on reviews by Jesse ("Jay") Taylor and 1 anonymous reviewerOf the four evolutionary forces, three can be straightforwardly summarized both conceptually and mathematically in the context of an allele at a genomic locus. Mutation (the mutation rate, μ) is simply captured by the per-site, per-generation probability that an allele mutates into a different allele. Recombination (the recombination rate, r) is captured as the probability of recombination between two sites, wherein alleles that are in different genomes in one generation come together in the same genome in the next generation. Natural selection (the selection coefficient, s) is captured by the probability that an allele is present in the next generation, relative to some reference.
Random genetic drift – the random fluctuation in allele frequency due to sampling in a finite population - is not so straightforwardly summarized. The first, and most common way of characterizing evolutionary dynamics in a finite population is the Wright-Fisher model, in which the only deviation from the assumptions of Hardy-Weinberg conditions is finite population size. Importantly, in a W-F population, mating between diploid individuals is random, which implies self-fertile monoecy, and generations are non-overlapping. In an ideal W-F population, the probability that a gene copy leaves i descendants in the next generation is the result of binomial sampling of uniting gametes (if the locus is biallelic). The – and the next word is meaningful – magnitude/strength/rate/power/amount of genetic drift is proportional to 1/2N, where N is the size of the population. All of the following are affected by genetic drift: (1) the probability that a neutral allele ultimately reaches fixation, (2) the rate of loss of genetic variation within a population, (3) the rate of increase of genetic variance among populations, (4) the amount of genetic variation segregating in a population, (5) the probability of fixation/loss of a weakly selected variant.
Presumably no real population adheres to ideal W-F conditions, which leads to the notion of "effective population size", Ne (Wright 1931), loosely defined as "the size of an ideal W-F population that experiences an equivalent strength of genetic drift". Almost always, Ne<N, and any violation of W-F assumptions can affect Ne. Importantly, Ne can be defined in different ways, and the specific formulation of Ne can have different implications for evolution. Ne was initially defined in terms of the rate of decrease of heterozygosity (inbreeding effective size) and increase in variance among populations (variance effective size). Ewens (1979) defined the Eigenvalue effective size (equivalent to the "random extinction" effective size) and elaborated on the conditions under which the various formulations of Ne differ (Ewens 1982). Nordborg and Krone (2002) defined the effective size in terms of the coalescent, and they identified conditions in which genetic drift cannot be described in terms of a W-F model (Sjodin et al. 2005); also see Karasov et al. (2010); Neher and Shraiman (2011).
Distinct from the issue of defining Ne is the issue of calculating Ne from data, which is the focus of this paper by De Meeus and Noûs (2023). Pudovkin et al. (1996) showed that the Eigenvalue effective size in a dioecious population can be formulated in terms of excess heterozygosity, which the current authors note is equivalent to formulating Ne in terms of Wright's FIS statistic. As emphasized by the title, the marquee contribution of this paper is to provide a better approximation of the Eigenvalue effective size in a dioecious population. Science marches onward, although the empirical utility of this advance is obviously limited, given the tremendous inherent sources of uncertainty in real-world estimates of Ne. Perhaps more valuable, however, is the extensive set of appendixes, in which detailed derivations are provided for the various formulations of effective size. By way of analogy, the material presented here can be thought of as an extension of the material presented in section 7.6 of Crow and Kimura (1970), in which the Inbreeding and Variance effective population sizes are derived and compared. The appendixes should serve as a handy go-to source of detailed theoretical information with respect to the different formulations of effective population size.
REFERENCES
Crow, J. F. and M. Kimura. 1970. An Introduction to Population Genetics Theory. The Blackburn Press, Caldwell, NJ.
De Meeûs, T. and Noûs, C. 2023. A new and almost perfectly accurate approximation of the eigenvalue effective population size of a dioecious population: comparisons with other estimates and detailed proofs. Zenodo, ver. 6 peer-reviewed and recommended by Peer Community in Evolutionary Biology. https://doi.org/10.5281/zenodo.7927968
Ewens, W. J. 1979. Mathematical Population Genetics. Springer-Verlag, Berlin.
Ewens, W. J. 1982. On the concept of the effective population size. Theoretical Population Biology 21:373-378. https://doi.org/10.1016/0040-5809(82)90024-7
Karasov, T., P. W. Messer, and D. A. Petrov. 2010. Evidence that adaptation in Drosophila Is not limited by mutation at single sites. Plos Genetics 6. https://doi.org/10.1371/journal.pgen.1000924
Neher, R. A. and B. I. Shraiman. 2011. Genetic Draft and Quasi-Neutrality in Large Facultatively Sexual Populations. Genetics 188:975-U370. https://doi.org/10.1534/genetics.111.128876
Nordborg, M. and S. M. Krone. 2002. Separation of time scales and convergence to the coalescent in structured populations. Pp. 194–232 in M. Slatkin, and M. Veuille, eds. Modern Developments in Theoretical Population Genetics: The Legacy of Gustave Malécot. Oxford University Press, Oxford. https://www.webpages.uidaho.edu/~krone/malecot.pdf
Pudovkin, A. I., D. V. Zaykin, and D. Hedgecock. 1996. On the potential for estimating the effective number of breeders from heterozygote-excess in progeny. Genetics 144:383-387. https://doi.org/10.1093/genetics/144.1.383
Sjodin, P., I. Kaj, S. Krone, M. Lascoux, and M. Nordborg. 2005. On the meaning and existence of an effective population size. Genetics 169:1061-1070. https://doi.org/10.1534/genetics.104.026799
Wright, S. 1931. Evolution in Mendelian populations. Genetics 16:0097-0159. https://doi.org/10.1093/genetics/16.2.97

Masculinization of the X-chromosome in aphid soma and gonads
Sex-biased gene expression is not tissue-specific in Pea Aphids
Recommended by Charles Baer and Tanja Schwander based on reviews by Ann Kathrin Huylmans and 1 anonymous reviewerSexual antagonism (SA), wherein the fitness interests of the sexes do not align, is inherent to organisms with two (or more) sexes. SA leads to intra-locus sexual conflict, where an allele that confers higher fitness in one sex reduces fitness in the other [1, 2]. This situation leads to what has been referred to as "gender load", resulting from the segregation of SA alleles in the population. Gender load can be reduced by the evolution of sex-specific (or sex-biased) gene expression. A specific prediction is that gene-duplication can lead to sub- or neo-functionalization, in which case the two duplicates partition the function in the different sexes. The conditions for invasion by a SA allele differ between sex-chromosomes and autosomes, leading to the prediction that (in XY or XO systems) the X should accumulate recessive male-favored alleles and dominant female-favored alleles; similar considerations apply in ZW systems ([3, but see 4].
Aphids present an interesting special case, for several reasons: they have XO sex-determination, and three distinct reproductive morphs (sexual females, parthenogenetic females, and males). Previous theoretical work by the lead author predict that the X should be optimized for male function, which was borne out by whole-animal transcriptome analysis [5].
Here [6], the authors extend that work to investigate “tissue”-specific (heads, legs and gonads), sex-specific gene expression. They argue that, if intra-locus SA is the primary driver of sex-biased gene expression, it should be generally true in all tissues. They set up as an alternative the possibility that sex-biased gene expression could also be driven by dosage compensation. They cite references supporting their argument that "dosage compensation (could be) stronger in the brain", although the underlying motivation for that argument appears to be based on empirical evidence rather than theoretical predictions.
At any rate, the results are clear: all tissues investigated show masculinization of the X. Further, X-linked copies of gene duplicates were more frequently male-biased than duplicated autosomal genes or X-linked single-copy genes.
To sum up, this is a nice empirical study with clearly interpretable (and interpreted) results, the most obvious of which is the greater sex-biased expression in sexually-dimorphic tissues. Unfortunately, as the authors emphasize, there is no general theory by which SA, variable dosage-compensation, and meiotic sex chromosome inactivation can be integrated in a predictive framework. It is to be hoped that empirical studies such as this one will motivate deeper and more general theoretical investigations.
References
[1] Rice WR, Chippindale AK (2001) Intersexual ontogenetic conflict. Journal of Evolutionary Biology 14: 685-693. https://doi.org/10.1046/j.1420-9101.2001.00319.x
[2] Bonduriansky R, Chenoweth SF (2009) Intralocus sexual conflict. Trends Ecol Evol 24: 280-288. https://doi.org/10.1016/j.tree.2008.12.005
[3] Rice WR. (1984) Sex chromosomes and the evolution of sexual dimorphism. Evolution 38: 735-742. https://doi.org/10.1086/595754
[4] Fry JD (2010) The genomic location of sexually antagonistic variation: some cautionary comments. Evolution 64: 1510-1516. https://doi.org/10.1111%2Fj.1558-5646.2009.00898.x
[5] Jaquiéry J, Rispe C, Roze D, Legeai F, Le Trionnaire G, Stoeckel S, et al. (2013) Masculinization of the X Chromosome in the Pea Aphid. PLoS Genetics 9. https://doi.org/10.1371/journal.pgen.1003690
[6] Jaquiéry J, Simon J-C, Robin S, Richard G, Peccoud J, Boulain H, Legeai F, Tanguy S, Prunier-Leterme N, Le Trionnaire G (2022) Masculinization of the X-chromosome in aphid soma and gonads. bioRxiv, 2021.08.13.453080, ver. 4 peer-reviewed and recommended by Peer Community in Evolutionary Biology. https://doi.org/10.1101/2021.08.13.453080

Sexual selection and inbreeding: two efficient ways to limit the accumulation of deleterious mutations
Inbreeding compensates for reduced sexual selection in purging deleterious mutations
Recommended by Charles Baer based on reviews by 2 anonymous reviewersTwo evolutionary processes have been shown in theory to enhance the effects of natural selection in purging deleterious mutations from a population (here ""natural"" selection is defined as ""selection other than sexual selection""). First, inbreeding, especially self-fertilization, facilitates the removal of deleterious recessive alleles, the effects of which are largely hidden from selection in heterozygotes when mating is random. Second, sexual selection can facilitate the removal of deleterious alleles of arbitrary dominance, with little or no demographic cost, provided that deleterious effects are greater in males than in females (""genic capture""). Inbreeding (especially selfing) and sexual selection are often negatively correlated in nature. Empirical tests of the role of sexual selection in purging deleterious mutations have been inconsistent, potentially due to the positive relationship between sexual selection and intersexual genetic conflict.
In their preprint, Noël et al. [1] report a cleverly designed, and impressively long-term, experimental evolution study designed to tease apart the relative contributions of selfing and sexual selection in purging deleterious mutations, using the self-compatible hermaphroditic snail Physa acuta. Hermaphroditism relieves at least some of the potential conflict between males and females because each individual expresses traits of each sex. The authors report a 50-generation (ten years!) evolution experiment with four experimental treatments: Control (C), in which snails reproduced by mass mating (allowing sexual selection) and the next generation was sampled randomly from offspring in proportion to maternal family size; Male-selection (M) in which snails reproduced by mass mating but maternal family size was held constant, removing the opportunity for fertility selection; Female fertility selection (F) in which snails mated monogamously but fertility selection was imposed, and selfing (S), in which snails reproduced by selfing every other generation, alternating with monogamy + fertility selection. Juvenile survival was taken as the proxy for fitness and was measured for offspring of self-fertilization and of outcross matings. Each line type (C, M, F, S) was replicated twice.
The results are enviably clear-cut: after 50 generations of evolution, outcross fitness dropped precipitously in the F treatment (monogamy+female fertility selection) and remained at ancestral levels in the other three treatments. Clearly, sexual selection in males is more efficient at purging deleterious alleles than is female fertility selection. Similarly, inbreeding depression was reduced in the S lines relative to the other treatments, indicating that, unsurprisingly, deleterious recessive mutations of large effect are purged under strong inbreeding. Outcross fitness in the S lines did not decline, in contrast to the F lines, which indicates that deleterious mutations are on average slightly recessive.
Taken as a whole, this study by Noël et al. [1] provides a compelling empirical demonstration of the efficacy of both sexual selection and strong inbreeding as mechanisms of purging, and implicates sexual conflict as a potentially important factor in studies in which relaxation of sexual selection fails to result in purging.
References
[1] Noël, E., Fruitet, E., Lelaurin, D., Bonel, N., Segard, A., Sarda, V., Jarne, P., & David P. (2018). Sexual selection and inbreeding: two efficient ways to limit the accumulation of deleterious mutations. bioRxiv, 273367, ver. 3 recommended and peer-reviewed by PCI Evol Biol. doi: 10.1101/273367