
Disentangling the impact of mating and competition on dispersal patterns
Exploring the effects of ecological parameters on the spatial structure of genetic tree sequences
Abstract
Recommendation: posted 22 February 2024, validated 23 February 2024
Ortega-Del Vecchyo, D. (2024) Disentangling the impact of mating and competition on dispersal patterns. Peer Community in Evolutionary Biology, 100655. https://doi.org/10.24072/pci.evolbiol.100655
Recommendation
Spatial population genetics is a field that studies how different evolutionary processes shape geographical patterns of genetic variation. This field is currently hampered by the lack of a deep understanding of the impact of different evolutionary processes shaping the genetic diversity observed across a continuous space (Bradburd and Ralph 2019). Luckily, the recent development of slendr (Petr et al. 2023), which uses the simulator SLiM (Haller and Messer 2023), provides a powerful tool to perform simulations to analyze the impact of different evolutionary parameters on spatial patterns of genetic variation. Here, Ianni-Ravn, Petr, and Racimo 2023 present a series of well-designed simulations to study how three evolutionary factors (dispersal distance, competition distance, and mate choice distance) shape the geographical structure of genealogies.
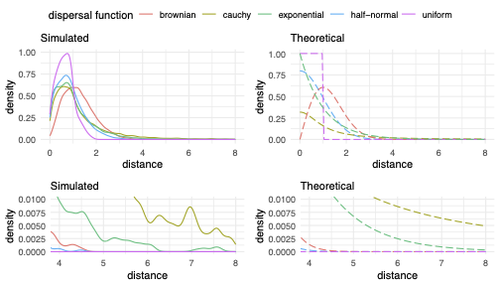
The authors model the dispersal distance between parents and their offspring using five different distributions. Then, the authors perform simulations and they contrast the correspondence between the distribution of observed parent-offspring distances (called DD in the paper) and the distribution used in the simulations (called DF). The authors observe a reasonable correspondence between DF and DD. The authors then show that the competition distance, which decreases the fitness of individuals due to competition for resources if the individuals are close to each other, has small effects on the differences between DD and DF. In contrast, the mate choice distance (which specifies how far away can a parent go to choose a mate) causes discrepancies between DD and DF. When the mate choice distance is small, the individuals tend to cluster close to each other. Overall, these results show that the observed distances between parents and offspring are dependent on the three parameters inspected (dispersal distance, competition distance, and mate choice distance) and make the case that further ecological knowledge of each of these parameters is important to determine the processes driving the dispersal of individuals across geographical space. Based on these results, the authors argue that an “effective dispersal distance” parameter, which takes into account the impact of mate choice distance and dispersal distance, is more prone to be inferred from genetic data.
The authors also assess our ability to estimate the dispersal distance using genealogical data in a scenario where the mating distance has small effects on the dispersal distance. Interestingly, the authors show that accurate estimates of the dispersal distance can be obtained when using information from all the parents and offspring going from the present back to the coalescence of all the individuals to the most recent common ancestor. On the other hand, the estimates of the dispersal distance are underestimated when less information from the parent-offspring relationships is used to estimate the dispersal distance.
This paper shows the importance of considering mating patterns and the competition for resources when analyzing the dispersal of individuals. The analysis performed by the authors backs up this claim with carefully designed simulations. I recommend this preprint because it makes a strong case for the consideration of ecological factors when analyzing the structure of genealogies and the dispersal of individuals. Hopefully more studies in the future will continue to use simulations and to develop analytical theory to understand the importance of various ecological processes driving spatial genetic variation changes.
References
Bradburd, Gideon S., and Peter L. Ralph. 2019. “Spatial Population Genetics: It’s About Time.” Annual Review of Ecology, Evolution, and Systematics 50 (1): 427–49. https://doi.org/10.1146/annurev-ecolsys-110316-022659.
Haller, Benjamin C., and Philipp W. Messer. 2023. “SLiM 4: Multispecies Eco-Evolutionary Modeling.” The American Naturalist 201 (5): E127–39. https://doi.org/10.1086/723601.
Ianni-Ravn, Mariadaria K., Martin Petr, and Fernando Racimo. 2023. “Exploring the Effects of Ecological Parameters on the Spatial Structure of Genealogies.” bioRxiv, ver. 3 peer-reviewed and recommended by Peer Community in Evolutionary Biology. https://doi.org/10.1101/2023.03.27.534388.
Petr, Martin, Benjamin C. Haller, Peter L. Ralph, and Fernando Racimo. 2023. “Slendr: A Framework for Spatio-Temporal Population Genomic Simulations on Geographic Landscapes.” Peer Community Journal 3 (e121). https://doi.org/10.24072/pcjournal.354.
The recommender in charge of the evaluation of the article and the reviewers declared that they have no conflict of interest (as defined in the code of conduct of PCI) with the authors or with the content of the article. The authors declared that they comply with the PCI rule of having no financial conflicts of interest in relation to the content of the article.
FR was supported by a Villum Young Investigator Grant (project no. 00025300), a COREX ERC Synergy grant (ID 951385) and a Novo Nordisk Fonden Data Science Ascending Investigator Award (NNF22OC0076816). MP was supported by a Lundbeck Foundation grant (R302-2018-2155) and a Novo Nordisk Foundation grant (NNF18SA0035006) given to the GeoGenetics Centre.
Evaluation round #1
DOI or URL of the preprint: https://doi.org/10.1101/2023.03.27.534388
Version of the preprint: 2
Author's Reply, 28 Dec 2023
Dear Dr Ortega-Del Vecchyo,
We have been working to revise our manuscript, “Exploring the Effects of Ecological Parameters on the Spatial Structure of Genealogies”, in response to your comments, and here upload an updated version. We thank you, and all the referees for your time and work - we strongly believe that the critique provided has led to significant improvements in the manuscript.
We have responded to each of the comments, and provide point-by-point responses below. The line numbers refer to the revised version. Additionally, we have amended the order of some of the figures, and shifted two to be supplementary material. For simplicity, we keep these in the same document.
Furthermore, to comply with PCI requirements, we have added a conflict of interest disclosure section, and have supplied a perennial URL (https://zenodo.org/doi/10.5281/zenodo.10402648) for the scripts used in the analysis.
All the best,
Mariadaria Ianni-Ravn
Decision by Diego Ortega-Del Vecchyo, posted 13 Jun 2023, validated 14 Jun 2023
Dear Mariadaria K. Ianni-Ravn and coauthors,
Four reviewers and myself have read your paper and we have found that your work is a great contribution to understand the impact of various phenomena on patterns of spatial genetic variation. The reviewers and I have some comments that would be good to address. If you are interested, I would like to consider a revised version of the manuscript for recommendation after taking into account all the comments into account.
All the best,
Diego
Comments:
The number of the figures should be mentioned on the text in an ascending order starting from Figure 1. Figure 2 is referenced before Figure 1 on the text.
Figure 2.- “the right one gives the shape of the corresponding dispersal distributions.” The legend at the top of the right panel figures state that these are “Theoretical”. Unsure about what are the right panels showing.
Figure 2.- Could the authors state more precisely what is the difference between the two top panels and the two bottom panels?
Line 120.- “The shape of the DDd was related to that of the theoretical DF”. It would be nice to give a line or two explaining how the theoretical DF was derived and pointing to the reader to the place on the manuscript showing where they can find the derivation of these results.
Figure 7.- I would suggest to have results for alternative values of sigma to check the accuracy of the estimate for alternative values of this parameter.
Figure 8 is not referenced on the text.
Reviewed by anonymous reviewer 1, 01 Jun 2023
Reviewed by Anthony Wilder Wohns, 22 May 2023
Ianni-Ravn, Petr, and Racimo have contributed a timely and insightful manuscript that seeks to disentangle the relationship between theoretical dispersal distributions, mate choice and spatial competition. The forward simulators SLiM and slendr have allowed researchers to perform complex spatial simulations, but have also highlighted gaps in our understanding of the influence of ecological parameters on spatial dynamics. The authors thus undertook a carefully designed simulation study to understand the interaction between these parameters.
The authors provide useful theoretical results with sensible parameterizations of parent-offspring dispersal distance functions. They explore the effects of the dispersal variance parameter in simulations, with expected results. Varying the scale of competition is observed to affect clustering, while mate choice boundaries modify dispersal distances. They also make the important observation that long branch lengths can lead to inference biases in the setting of finite habitat size.
The complexities of these problems are not to be underestimated, and I appreciate that the authors took care to explore a well-defined and approachable slice of the parameter space. There is clearly significant scope for more work in this area.
I have the following specific comments for the authors:
- Section 5.1.2 states "We simulated a single locus in order to focus on fundamental geographic dynamics which act on single trees". It thus appears that all simulation work was performed on single locus trees, not ARGs or tree sequences. I would suggest the title be amended to reflect this salient point, as recombination can introduce complexities which are not explored in this work. The results are still quite relevant for understanding the spatiotemporal dynamics of recombining organisms, but it could be misleading for readers to assume that tree sequences, rather than single trees, are explored here.
- The abstract states the paper will examine how the parameters studied "influence the distance between closely- and distantly-related individuals in these genealogies". However, the results focus on the distribution of parent-offspring relations only. Similarly, the structure of the genealogies themselves are not a focus of the work, aside from the observation that long-range competition led to clustering. I would suggest the abstract be modified to better reflect the scope of the work performed. Furthermore, it would be helpful to highlight some of the concrete theoretical and empirical results of the work in the abstract, for instance the effect of competition and mate choice on the dispersal distances, and/or the importance of habitat size in inference.
- Regarding the introduction, it should be clarified that the work was not performed with ARGs/tree sequences, though it has important relevance to work in that area. Furthermore, the definitions and usage of the terms phylogenies, pedigrees, genealogical trees, ancestral recombination graphs, and tree sequences could be more precise. For instance, paragraph 5 of the introduction states "With some loss of information, an ARG can be further simplified into a sequence of trees along the genome". What specific information are the authors referring to, and how is this relevant? It's unclear from the text why the authors consider tree sequences to be theoretically more amenable for inference than ARGs. Additionally the brief description of tree sequences leaves the impression that they are simply a sequence of unrelated local genealogical trees. These subtleties are especially important since the work in this manuscript does not operate on tree sequences, so its relevance here should be more clearly argued.
- There is a minor error in the citation of Kelleher, Wong, et al. 2019., which should be Kelleher et al. 2019. Also, Wohns et al. 2021 refers to the preprinted version of a manuscript published in 2022.
- Two very minor points on simulation size: I don't think this would change any results, but the tails of the simulated distance distribution in Figure 2 would appear cleaner with a few more replicates. This shouldn't be too onerous as it appears the simulations were not very computationally intensive. Also, using different icons for the replicates in figure 7 is not necessary as the data points are overplotted anyway.
- I believe there is an error in the reference to Fig. 7 in the last sentence of the results, it appears the analysis described in this paragraph should refer to Fig. 8?
- I greatly enjoyed reading the discussion in particular, which I thought had a number of very important and practical points. It might be helpful to outline other important, but currently underexplored questions. One is the possible consequences of using tree sequences rather than marginal trees in these analyses. Another is the biases which could be introduced by using inferred rather than simulated trees.
- Typo in line 295 "ecah".
It is my opinion that the technical aspects of this work are sound and that it will prove valuable to the growing number of researchers interested in spatial population genetics. I congratulate the authors on their work!
https://doi.org/10.24072/pci.evolbiol.100655.rev12Reviewed by anonymous reviewer 2, 20 May 2023
In this paper the authors examine the effect of three functions -- the dispersal kernel, the mate choice kernel, and the competition kernel (fig 1) -- on the distance a sampled genetic lineage moves from one generation to the next (fig 2, 3, 5, 6, hereafter "realized parent-offspring distances"), spatial clumping (fig 4), and maximum likelihood estimates of the dispersal rate (fig 7, 8). They do this via individual-based simulations (section 5.1) and math (section 5.3). One key finding is that while local competition tended to decrease the probability of small realized parent-offspring distance (fig 2) and affect spatial clumping (fig 4), it had a much smaller effect on the variance in realized offspring-parent distances than the mate choice kernel (fig 5), which dramatically affected the distribution of realized parent-offspring distances (fig 6) and the resulting dispersal estimates (fig 8). A second key finding is that habitat boundaries cause underestimates of the dispersal rate, but this can be corrected by ignoring long branches (fig 7). And a third key finding is that the shape of the dispersal kernel affects estimates of the dispersal rate (fig 8). Together, the authors show here that all three kernels affect spatial patterns in relatedness, which is important to keep in mind when interpreting estimates of "effective" dispersal rates.
L58-64: You introduce the dispersal distribution, the idea that we can estimate a dispersal distance, and that the ARG might be useful. You then say that two recent methods use the ~ARG to locate genetic ancestors. The idea of locating ancestors seems to come out of nowhere to me, and is not examined in this paper. I think it would be more appropriate to here discuss that dispersal distance can be estimated from a tree (and tree sequences). If you want to discuss locating ancestors then a bit more context is needed, I think, to connect to the rest of the paper, especially since under a model of Brownian motion the most likely location of an ancestor doesn't actually depend on the dispersal distance (though the confidence interval does).
L66-68: The comment "... little work has been done to assess how spatial parameters ... affect a tree sequence" is a little vague to me, making it hard to determine how much previous work has been done. (You could say something more specific instead, like the distance between parents and offspring in sample lineages and/or estimates of the dispersal distance from a tree.) While they don't use trees, Smith et al (https://www.biorxiv.org/content/10.1101/2022.08.25.505329v5) do look at the effect of mate and competition kernels on dispersal estimates (their supp fig 1), coming to the same conclusion that competition has a much weaker effect than mate choice (they use SLiM too).
L81: Why did you choose to use slendr and not just SLiM? My understanding is that slendr is a great help when working with complex spatial habitats (eg, real world maps) and population structure (eg, population splits and admixture), but here the simulations are a homogenous square with a single population. Wouldn't using SLiM directly make it easier to vary kernels, like mate choice (whereas it sounds like slendr forces this to be uniform, L113-114)?. I'm guessing the answer has something to do with sf (section 5.1.3)?
L104-106: "... the faster the population spreads across the landscape" makes it sound like you are simulating a range expansion. I don't think you give any information about the initial conditions of the simulation, but my guess is that the first generation is placed uniformly at random, in which case this isn't an expansion. Perhaps, "... the faster genetic lineages spread across the landscape" would be more appropriate?
L117: "... sampled all individuals and reconstructed the tree connecting them" makes it sound like you inferred the tree that relates individual to one another. I would have thought instead you simply saved the tskit tree sequence recorded by SLiM. If this is correct, there is also some imprecision in the word "them" (referring to individuals, which I presume are diploid), since a tree sequence connects haploid genomes (in this case alleles). The relations between the individuals can be described by a pedigree, but that is not generally a tree. Some clarification needed I think.
L132-137: You give a specific value of the competition distance that you say reduces clumping and scattering and excess variance in dispersal distances (0.2) but then say this is not a general finding. Maybe remove the emphasis on the exact value (0.2) and instead refer to "an intermediate" value of competition distance?
L129-137: I'm not sure I see the changes in clumping with competition distance that you describe in Fig 4. To me it looks like competition distance has very little impact on clumping and instead it is mating distance that determines how many clumps you can have (and how connected they are). I think this might be connected to what Felsenstein (1975 Am Nat) showed, that you get clusters when you impose a constant population size (his eqn 13). This is long-range competition and is acting in all of your (Wright-Fisher) simulations, regardless of the competition distance. One way to avoid clumping, then, is to simulate a non-Wright-Fisher population with population size controlled dynamically by local competition. I'm not suggesting you re-do the simulations, I'm just looking for a clearer explanation of the patterns in fig 4. The fact that competition does not affect clumping as much as mate choice does may also help explain why competition has much less effect on realized parent-offspring distances and effective dispersal estimates?
Fig 2: It would have helped me if you stated what "simulated distances" means right here in the caption (this is a general comment, since many readers will want to look at the figures and caption without having to repeatedly read the main text). Naively one might think these distances are just draws from the chosen theoretical distribution (given in the right panel), but I think they are instead the distances each sampled genetic lineage moved from one generation to the next, which is influenced by both competition and mate choice.
L161-163: As a side note, the fact that the math works out easier with Gaussians is one of the reasons (the other being biological realism) that I'm surprised slendr uses uniform mate choice and comeptition kernels. But I guess there is an argument to be made for computational speed?
L167 (and L169): I think the \pi should be \sqrt(\pi).
Eqn 4: I think there is an error in this equation: shouldn't the sum be of d_i^2/l_i, which gives the appropriate units of distance/sqrt(time)? This can be derived by setting \tau=0 in Eqn 3, replacing \sigma^2 with l_i\sigma^2 (ie, the variance increases linearly with time under Brownian motion), taking the product of g_{y_i}(y_i) over i from 1 to N, differentiating with respect to \sigma, setting the derivative equal to zero, and solving for \sigma. It looks like estimation.R uses the correct equation, so I think this is just a typo (and explains why the estimates do well in the figures).
L174: Is this still a population of size 50 (ie, you are sampling every haploid genome)? estimation.R makes me think N=2000 here, which might be good to state in the main text.
L178-180: It might be helpful to state what l_i is for the tips-only case, since there are multiple branches involved. I think it is 2TMRCA? This would also help clarify what it means to 'cut' branches in the tips only case. One issue here is that, while the distance between two samples follows a Rayleigh distribution, that distance is not necessarily independent of the distance between another pair of samples (if there are shared branches between the two pairs). This means that Eqn 4 maximizes the composite likelihood. However I think it also maximizes the true likelihood in this case, since the covariance between the distances from multiple pairs of samples is a nuisance parameter? I think this is one place in the paper where it would have helped me to see the connections between your work (in terms of absolute distances between pairs of nodes, which is Rayleigh when \tau=0) and previous approaches that instead model the locations of all nodes as a multivariate normal (eg, Osmond and Coop 2021, and the equivalent method of Felsenstein 1985). I guess they give equivalent dispersal estimates but the multivariate approach appropriately deals with covariance, and hence gives the correct likelihood function?
L182-185: I would say "adopted an approach similar to" or "inspired by" Osmond and Coop 2021, as they didn't explicitly ignore long branches but instead cut the entire tree off at some time in the past. I guess the methods do something quite similar when using tips-only (ignoring pairs of samples with 2TMRCA above a cut-off) but reasonably different when using a simplified tree (Osmond and Coop removed old branches while here you remove long branches).
L191: Fig 7 -> Fig 8
L203: I would like to hear why you think the estimated dispersal distance is more sensitive to mating distance with a Cauchy dispersal distribution.
Fig 7: I think it would be more intutive to order the figure, from left to right: unsimplified -> simplified -> tips only. This is the order discussed in the text, goes from most to least data, and shows a more or less linear decline in (naive) estimates of dispersal distance.
L208-210: "... altering the kernel of parent-offspring dispersal can have profound effects on the diffusion captured within a genealogy ...". I think the word "profound" is a little strong for a large but very expected result.
L217-220: Do you have a dispersal distribution in mind where the tail is independent of the variance?
L248-251: The Smith et al paper I mentioned earlier calculates a similar effective dispersal distance (see the simulation section of their methods), and use it to train their machine learning algorithm to estimate the true dispersal distance, which might be interesting to compare to.
L249: I -> we
L253-256: I like this point, that a non-zero mating distance will make the distribution of distances non-Rayleigh (or, as I tend to think about it, the signed distances will be non-Gaussian), making parameter estimation more complicated, but over long time periods the central limit theorem will cause the distances to become Gaussian (as will the signed distances) with a readily calculable effective dispersal distance.
L295: ecah -> each
L296: randomly at each generation -> randomly
L298: these -> populations
L309: are -> is
Fig 9: "(c) Each panel shows a slice of 250 generations" -- do you mean each color?
L323: grammar not right here
Eqn 10: Why is the first factor not 1/(2\pi)? I thought the angle was uniformly distributed over [0,2\pi] -- did a 2 get cancelled from elsewhere?
L386: In fact, you can get any moment of y from that expression.
Eqn 12: I think the f_y term should be multiplied by y as well.
Eqn 12: r_y is undefined.
L404: I'm confused by this 1-branch estimate of sigma. Why use a moment-based estimator to find out how much a branch contributes to the max likelihood estimator? Wouldn't it be more appropriate to set N=1 in Eqn 15, giving the max likelihood estimate d/\sqrt(2l)? Or better yet, if you look for the max likelihood estimate of \sigma^2, which is unbiased for a Rayleigh (Wikipedia), then d^2/(2Nl) is precisely how much each branch contributes to the overall max likelihood estimate.
https://doi.org/10.24072/pci.evolbiol.100655.rev13









