
DUTHEIL Julien Yann
- Theoretical Biology, Max Planck Institute for Evolutionary Biology, Plon, Germany
- Bioinformatics & Computational Biology, Genome Evolution, Human Evolution, Molecular Evolution, Phylogenetics / Phylogenomics, Population Genetics / Genomics
- recommender, manager, administrator
Recommendation: 1
Reviews: 0
Recommendation: 1
Simultaneous Inference of Past Demography and Selection from the Ancestral Recombination Graph under the Beta Coalescent
Beyond the standard coalescent: demographic inference with complete genomes and graph neural networks under the beta coalescent
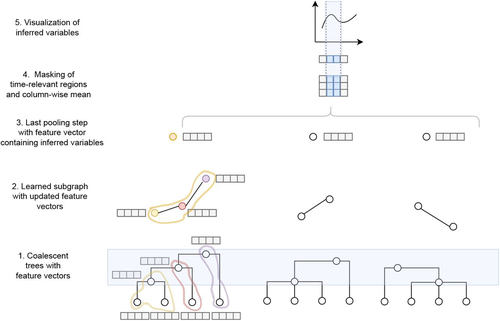
Recommended by Julien Yann Dutheil based on reviews by 2 anonymous reviewersModelling the evolution of complete genome sequences in populations requires accounting for the recombination process, as a single tree can no longer describe the underlying genealogy. The sequentially Markov coalescent (SMC, McVean and Cardin 2005; Marjoram and Wall 2006) approximates the standard coalescent with recombination process and permits estimating population genetic parameters (e.g., population sizes, recombination rates) using population genomic datasets. As such datasets become available for an increasing number of species, more fine-tuned models are needed to encompass the diversity of life cycles of organisms beyond the model species on which most methods have been benchmarked.
The work by Korfmann et al. (Korfmann et al. 2024) represents a significant step forward as it accounts for multiple mergers in SMC models. Multiple merger models account for simultaneous coalescence events so that more than two lineages find a common ancestor in a given generation. This feature is not allowed in standard coalescent models and may result from selection or skewed offspring distributions, conditions likely met by a broad range of species, particularly microbial.
Yet, this work goes beyond extending the SMC, as it introduces several methodological innovations. The "classical" SMC-based inference approaches rely on hidden Markov models to compute the likelihood of the data while efficiently integrating over the possible ancestral recombination graphs (ARG). Following other recent works (e.g. Gattepaille et al. 2016), Korfmann et al. propose to separate the ARG inference from model parameter estimation under maximum likelihood (ML). They introduce a procedure where the ARG is first reconstructed from the data and then taken as input in the model fitting step. While this approach does not permit accounting for the uncertainty in the ARG reconstruction (which is typically large), it potentially allows for the extraction of more information from the ARG, such as the occurrence of multiple merging events. Going away from maximum likelihood inference, the authors trained a graph neural network (GNN) on simulated ARGs, introducing a new, flexible way to estimate population genomic parameters.
The authors used simulations under a beta-coalescent model with diverse demographic scenarios and showed that the ML and GNN approaches introduced can reliably recover the simulated parameter values. They further show that when the true ARG is given as input, the GNN outperforms the ML approach, demonstrating its promising power as ARG reconstruction methods improve. In particular, they showed that trained GNNs can disentangle the effects of selective sweeps and skewed offspring distributions while inferring past population size changes.
This work paves the way for new, exciting applications, though many questions must be answered. How frequent are multiple mergers? As the authors showed that these events "erase" the record of past demographic events, how many genomes are needed to conduct reliable inference, and can the methods computationally cope with the resulting (potentially large) amounts of required data? This is particularly intriguing as micro-organisms, prone to strong selection and skewed offspring distributions, also tend to carry smaller genomes.
References
Gattepaille L, Günther T, Jakobsson M. 2016. Inferring Past Effective Population Size from Distributions of Coalescent Times. Genetics 204:1191-1206.
https://doi.org/10.1534/genetics.115.185058
Korfmann K, Sellinger T, Freund F, Fumagalli M, Tellier A. 2024. Simultaneous Inference of Past Demography and Selection from the Ancestral Recombination Graph under the Beta Coalescent. bioRxiv, 2022.09.28.508873. ver. 5 peer-reviewed and recommended by Peer Community in Evolutionary Biology. https://doi.org/10.1101/2022.09.28.508873
Marjoram P, Wall JD. 2006. Fast "coalescent" simulation. BMC Genet. 7:16.
https://doi.org/10.1186/1471-2156-7-16
McVean GAT, Cardin NJ. 2005. Approximating the coalescent with recombination. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 360:1387-1393.
https://doi.org/10.1098/rstb.2005.1673