
Further questions on the meaning of effective population size
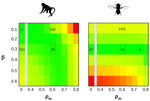
How much does Ne vary among species?
Abstract
Recommendation: posted 20 May 2020, validated 20 May 2020
Lascoux, M. (2020) Further questions on the meaning of effective population size. Peer Community in Evolutionary Biology, 100100. https://doi.org/10.24072/pci.evolbiol.100100
Recommendation
In spite of its name, the effective population size, Ne, has a complex and often distant relationship to census population size, as we usually understand it. In truth, it is primarily an abstract concept aimed at measuring the amount of genetic drift occurring in a population at any given time. The standard way to model random genetic drift in population genetics is the Wright-Fisher model and, with a few exceptions, definitions of the effective population size stems from it: “a certain model has effective population size, Ne, if some characteristic of the model has the same value as the corresponding characteristic for the simple Wright-Fisher model whose actual size is Ne” (Ewens 2004). Since Sewall Wright introduced the concept of effective population size in 1931 (Wright 1931), it has flourished and there are today numerous definitions of it depending on the process being examined (genetic diversity, loss of alleles, efficacy of selection) and the characteristic of the model that is considered. These different definitions of the effective population size were generally introduced to address specific aspects of the evolutionary process. One aspect that has been hotly debated since the first estimates of genetic diversity in natural populations were published is the so-called Lewontin’s paradox (1974). Lewontin noted that the observed variation in heterozygosity across species was much smaller than one would expect from the neutral expectations calculated with the actual size of the species.
In essence, what Galtier and Rousselle propose in their clever paper is to introduce a new approach to compare effective population sizes across species and thereby a new way to address Lewontin’s paradox. Classically, the effective population size in this type of comparative genomic studies is simply estimated from nucleotide diversity at putatively neutral sites using the equation relating levels of diversity (θ) to mutation rate per generation (μ) and effective population size, Ne, θ = 4Neμ. As Galtier and Rousselle point out there are many issues with this approach. In particular, although we can now estimate θ very precisely, we generally do not have a reliable estimate of the mutation rate, and the method rests on many, unwarranted, assumptions; for example that the population is at mutation-drift equilibrium. Instead they propose to estimate the effective population size from the load of segregating deleterious mutations which can be summarized by the ratio of nonsynonymous to synonymous mutations, πN/πS: small-Ne species are expected to accumulate more deleterious mutations and carry a higher load than large-Ne ones at selection/drift equilibrium (Ohta et al. 1973; Welch et al. 2008). At first glance, this suggestion seems counterintuitive since considering sites under selection undoubtedly adds a new layer of complexity to an already intricate situation. Indeed, one is now bringing to the brew another elusive object, namely, the Distribution of Fitness Effect of mutations (DFE). However, estimating Ne from the load of segregating deleterious mutations may actually simplify the situation in two important ways. First, using πN/πS does not require assumption about μ (as the mutation rate will cancel out in the ratio). Second, the ratio of nonsynonymous to synonymous nucleotide diversity, reaches equilibrium faster than the nucleotide diversity at synonymous site after a change in population size, so we can hope for less sensitivity to (often unknown) recent demographic history (Brandvain and Wright 2016).
Extending recent developments in the estimation of the DFE, Galtier and Rousselle eventually obtain estimates of the average deleterious effect, 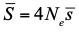 , where Ne is the effective population size and
, where Ne is the effective population size and  is the mean fitness effect of non-synonymous mutations. Assuming further that distinct species share a common DFE and therefore a common
is the mean fitness effect of non-synonymous mutations. Assuming further that distinct species share a common DFE and therefore a common  , they obtain estimates of the between species ratio of Ne from the between species ratio of
, they obtain estimates of the between species ratio of Ne from the between species ratio of  . Applying their newly developed approach to various datasets they conclude that the power of drift varies by a factor of at least 500 between large-Ne (Drosophila) and small-Ne species (H. sapiens). This is an order of magnitude larger than what would be obtained by comparing estimates of the variation in neutral diversity. Hence the proposed approach seems to have gone some way in making Lewontin’s paradox less paradoxical. But, perhaps more importantly, as the authors tersely point out at the end of the abstract their results further questions the meaning of Ne parameters in population genetics. And arguably this could well be the most important contribution of their study and something that is badly needed.
. Applying their newly developed approach to various datasets they conclude that the power of drift varies by a factor of at least 500 between large-Ne (Drosophila) and small-Ne species (H. sapiens). This is an order of magnitude larger than what would be obtained by comparing estimates of the variation in neutral diversity. Hence the proposed approach seems to have gone some way in making Lewontin’s paradox less paradoxical. But, perhaps more importantly, as the authors tersely point out at the end of the abstract their results further questions the meaning of Ne parameters in population genetics. And arguably this could well be the most important contribution of their study and something that is badly needed.
References
Brandvain Y, Wright SI (2016) The Limits of Natural Selection in a Nonequilibrium World. Trends in Genetics, 32, 201–210. doi: 10.1016/j.tig.2016.01.004
Ewens WJ (2010) Mathematical Population Genetics: Theoretical Introduction. Springer-Verlag New York Inc., New York, NY. doi: 10.1007/978-0-387-21822-9
Galtier N, Rousselle M (2020) How much does Ne vary among species? bioRxiv, 861849, ver. 4 peer-reviewed and recommended by PCI Evolutionary Biology. doi: 10.1101/861849
Lewontin RC (1974) The genetic basis of evolutionary change. Columbia University Press, New York.
Ohta T (1973) Slightly Deleterious Mutant Substitutions in Evolution. Nature, 246, 96–98. doi: 10.1038/246096a0
Welch JJ, Eyre-Walker A, Waxman D (2008) Divergence and Polymorphism Under the Nearly Neutral Theory of Molecular Evolution. Journal of Molecular Evolution, 67, 418–426. doi: 10.1007/s00239-008-9146-9
Wright S (1931) Evolution in Mendelian Populations. Genetics, 16, 97–159. url: https://www.genetics.org/content/16/2/97
The recommender in charge of the evaluation of the article and the reviewers declared that they have no conflict of interest (as defined in the code of conduct of PCI) with the authors or with the content of the article. The authors declared that they comply with the PCI rule of having no financial conflicts of interest in relation to the content of the article.
no declaration
Evaluation round #2
DOI or URL of the preprint: https://doi.org/10.1101/861849
Version of the preprint: 2
Author's Reply, 15 May 2020
Decision by Martin Lascoux, posted 03 May 2020
Dear authors,
I apologize for the delay in passing a decision due to one of the reviewers being sick and, unfortunately, eventually unable to send in the review. At the latest news the reviewer had to stay a short while at the hospital but is now feeling better. Fortunately, the other reviewer did a very thorough job and I will be happy to recommend the preprint after you have taken into account the minor changes that the reviewer suggested.
Best regards Martin Lascaux
Additional comments of the Managing board:
1) Mandatory modifications
As indicated in the 'How does it work?’ section and in the code of conduct, please make sure that:
-Data are available to readers, either in the text or through an open data repository such as Zenodo (free), Dryad or some other institutional repository. Data must be reusable, thus metadata or accompanying text must carefully describe the data.
-Details on quantitative analyses (e.g., data treatment and statistical scripts in R, bioinformatic pipeline scripts, etc.) and details concerning simulations (scripts, codes) are available to readers in the text, as appendices, or through an open data repository, such as Zenodo, Dryad or some other institutional repository. The scripts or codes must be carefully described so that they can be reused.
-Details on experimental procedures are available to readers in the text or as appendices.
-Authors have no financial conflict of interest relating to the article. The article must contain a "Conflict of interest disclosure" paragraph before the reference section containing this sentence: "The authors of this preprint declare that they have no financial conflict of interest with the content of this article." If appropriate, this disclosure may be completed by a sentence indicating that some of the authors are PCI recommenders: “XXX is one of the PCI XXX recommenders.”
2) when these changes are made, could you send us your MS in word or Latex format to contact@evolbiol.peercommunityin.org. We'll try to format it according to PCI requirements.
3) We will send it back to you for final verification and uploading to bioRxiv.
Reviewed by anonymous reviewer 2, 09 Apr 2020
I am grateful to the authors for taking my previous comments seriously. I think that the manuscript is much improved and remains interesting. Nevertheless, looking at the new Figure S7, I still have concerns about the legitimacy of estimating Ne from S_bar. If the authors agree, I think that the concerns should be emphasized more strongly. I also think that the authors could do more to show that the results could in principle be real. They need to show e.g. that a past bottleneck could lead to very large differences in the Ne values that apply to different statistics. Neither of these suggestions would require large changes.
- Can Sbar be used to estimate Ne when the ri vary?
In the very welcome new section 460-474, the authors come close to stating that their key statistic, Sbar has no clear meaning.
They argue that, with highly variable ri, “what exactly \theta measures in this case is unclear”. I think \theta does have a clear meaning: the mutation rate multiplied by the length of the terminal branches in the genealogies. But the meaning of S_bar really is unclear, because it affects predictions for all frequency classes.
The authors then argue that the realized ~3-fold variation in the ri estimates (0.5-1.5; Figure S7) "does not suggest to us that the ri's pose a major problem of comparability in this analysis." This statement seemed too confident to me. Because the ri do not apply to different epochs, but to branches across the entirely genealogy, I think that the 3-fold differences imply quite major departures from a standard neutral genealogy, and it is not clear how Sbar will behave in those cases. For example, I think Figure S7 implies lots of high frequency polymorphisms in the flies, which is suggestive of balancing selection or structure.
Currently, it is suggested that the reader can skip sections 1-3 of the discussion, but, unless the authors think my comments above are mistaken, I think that sections 4-5 need to clearly acknowledge the possibility that S_bar does not provide a meaningful estimate of Ne.
Smaller comments/suggestions:
The simulations.
The simulations should prove to the reader that non-equilibrium demography could lead to very large differences in the range Ne values as estimated from piS and Sbar. Currently, this is not very explicit from Figure 4. Also, I could not find a description of the bottleneck depth at generation 15,000.The introduction
The introduction should probably acknowledge the classical results showing that populations can be characterized by different values of Ne when the Wright-Fisher assumptions are violated (e.g “inbreeding effective size” vs “variance effective size” etc.). These differences are not very surprising in themselves. What is surprising is the very large (~10-fold) differences estimated in this work.“To our knowledge, the Gamma + lethal model has been tried in two studies before this one.” Didn’t Nielsen and Yang 2003 MBE also use this model?
In my previous comment 2.3, I asked whether the authors might attempt to estimate s_bar (i.e the mean selection coefficient unscaled by Ne). I think that previous authors have done this, and it relates to the interesting discussion in lines 631-635.
What are the CIs in Figure S7?
Is Kaiser and Charlesworth 2009 TIG relevant to the discussion of linked selection and mutation load? (lines 621-625).
l445: “can be interpreted as the relative effective mutation rate”. Could r_i be more clearly described as the relative length of the portions of the genealogies that lead to i tips?
There are two different legends for Figure 4 (pp. 35 and 39).
Grammar etc.
l38: "which implies to also infer" should be "which implies also inferring".
l51: "distribution of fitness effect[s]".
l72: "can as well be" should be "can also be".
l101: "by jointly analysis" should be "by jointly analyzing".
l242 and Figure 4. Does 2.10^4 mean 20,000? If so, notation could be clearer.
l243: 2.2 10^{-7} (missing multiplication sign).
l269: "we rather fitted" should be "we instead fitted"
l303 and l310: "probability to be observed" should be "probability of being observed"
l331: "Setting plth [set]".
l338: "colons" should be "columns".
l440: “parameters of nuisance” should be “nuisance parameters”.
l464: “in [the] absence of”.
l536: “implies to accommodate” should be “implies accommodating”.
l556: “did not change much the picture” should be “did not change the picture much”.
Evaluation round #1
DOI or URL of the preprint: 10.1101/861849
Version of the preprint: 1
Author's Reply, 13 Mar 2020
Decision by Martin Lascoux, posted 15 Jan 2020
Dear Dr Galtier,
Three reviewers have now read your manuscript "How much does Ne vary among species?". All three reviewers find the manuscript very interesting but all three think that the manuscript could be improved by clarifying its main aim. In particular, they would like you to (i) clarify what is being measured by the two estimates of Ne, (ii) improve the comparison of the different DFE models, (ii) extend the simulations. Once this is done it should be easier to present the different aims of the paper (compare different estimates of Ne, testing Lewontin paradox, assess the stability of the DFE across species) in a clearer way or refocus the manuscript.
I look forward to receive a revised version of the manuscript.
Best regards Martin Lascoux
Reviewed by anonymous reviewer 2, 23 Dec 2019
The effective size of a population is the census size of a Wright-Fisher population that would give the same value of some statistic, related to drift. When the Wright-Fisher assumptions are violated, different statistics can imply different values of Ne. Differences between different methods of estimating Ne (e.g. from mean time to pairwise coalescence, vs. total genealogy length) are interesting, because they tell us about violations of the Wright-Fisher assumptions, and because the different Ne values might affect different things (e.g. total neutral diversity vs. current efficacy of purifying selection).
This preprint compares the extent of differences in Ne, estimated in two ways. First, it uses piS, the mean pairwise differences at synonymous sites, where E(piS)=4Nemu. Second, it estimates S=4Nes using the non-synonymous and synonymous SFS. Estimates are obtained for a wide variety of animal species, but focussing on primates vs. Drosophila. Results show that S/min(S) is 1-2 orders of magnitude more variable than piS/min(piS). This is a surprising result, especially if the DFE is identical between species.
The authors relate their finding to Lewontin's paradox: the finding that genetic diversity between species varies much less than would be expected under an equilibrium neutral model, assuming that effective population sizes are proportional to current census sizes. The authors implicate non-equilibrium demography, because piS is strongly influenced by past periods of low population size, while piN/pi_S equilibrates more rapidly, and so should be less influenced by past demography. This point is illustrated with simulations.
The preprint presents interesting work on an important topic, but I think some major points need to be clarified and developed before the results can be properly understood.
1- What is being estimated?
This preprint compares two different types of Ne, but I think the authors could be much clearer about what they measure.
In the equation E(pi_S)=4Nemu, 2Ne describes the average time to coalescence of two randomly chosen sequences.
The method of Galtier (2016) estimates Ne in two different ways, via the compound parameters theta=4Nemu and S=4Ne*s. Only the second measure is reported, and I could not tell when/whether the two Ne values are expected to differ from each other, and whether the second measure (which is the only one reported) is a valid measure of Ne.
From eqs. 6 and 10 of Galtier 2016 with r1=1, it looks like 4Ne estimated from theta/mu measures the mean length of the terminal branches on the genealogy. With non-equilibrium demography, this could differ from the mean time to pairwise coalescence. The lengths of the internal branches are fit via the nuisance parameters (ri).
I found the other Ne (estimated from S/4s) much more difficult to interpret. S is estimated from the complete SFS of non-synonymous mutations. But it does not use existing results for the SFS with selection and non-equilibrium demography or linkage effects (e.g. Evans et al 2007 TPB; Good et al 2014 PLoS Genet). Instead, it uses the standard equilibrium formula for the population allele frequency (eq. 4 of Galtier 2016), while also allowing for non-equilibrium effects on the shape of the underlying genealogy, by allowing for arbitrary variation in the r_i.
For this reason, I struggled to understand what these Ne estimates meant, and whether all of the possible variation in the non-synonymous SFS could be modelled via variation in Ne, even assuming that the gamma+method DFE is accurate.
Because the variation in these Ne values is the major result of the paper, I think this needs to be clarified.
2- Model adequacy
Estimates of S are highly model-dependent, and the authors present some suggestive evidence that the standard gamma model underfits the SFS data. They use a gamma+lethal model and show that the extra parameter has a substantial influence on the estimates.
This is an interesting result, but I think that the authors might be too quick to assume that the gamma+lethal model solves the problem of model adequacy, and to conclude that there is little difference in the DFE across their data sets.
Previous authors have examined the adequacy of the gamma model, with different sorts of data, including Nielsen & Yang (2003, MBE) and Loewe and Charlesworth (2006, Biol Lett). Nielsen and Yang also used a gamma+lethal model (and a normal + lethal model), while Loewe and Charlesworth argued for a lognormal model. Other authors have combined a gamma distribution with a class of purely neutral mutations (Loewe et al 2006, Genetics; Betancourt et al. 2012 Evolution). It would be useful to know if results are robust to using other distributions like this. While Table 2 contains many good robustness analyses, I think more formal work on model adequacy could be presented to make the headline results really convincing.
Second, the authors argue that their estimated likelihood surface "suggests that the DFE perhaps does not differ so dramatically between primates and fruit flies", but doesn't this flat likelihood surface suggest instead that the parameters are non-identifiable with data of this kind?
Third, as the authors say, the results for Ne depend heavily on the very strong assumption that s_bar has the same value for one set of genes in Drosophila and a different set of genes in primates. Chen et al. 2017 and Loewe et al. 2006 present methods for estimating the strength of selection directly. Could these be used to test this strong assumption?
3- Simulations
Figure 4 presents simulation runs, aiming to show that piN/piS is less affected by demographic events than pi_S. This is an important part of the paper, but I was not sure how well the simulations related to the results reported.
First, the S estimates used the full SFS for non-synonymous and synonymous polymorphisms, while the simulations report piN/piS. These quantities might equilibrate differently (as is evident from Tajima's D).
Second, if I have understood correctly, the "recovery phase" shows a gain in genetic diversity starting from a large but genetically uniform population. Is this realistic? Why did the authors not explicitly simulate the recovery from a bottleneck?
Third, to place their results in context, the authors cite Brandvain and Wright 2016 regarding the different equilibration times of piN and piS. But I think the explanation of the simulation results might be that ratios of pairwise diversity equilibrate more rapidly than raw diversity measurements. This is seen in neutral Fst, for example (Pannell and Charlesworth 2002).
Finally, if the authors suspect that non-equilibrium effects explain some of their results, why do they not test for these effects directly in their data (e.g. by reporting the r_i from Galtier 2016, or Tajima's D for synonymous sites etc.)?
Minor suggestions:
The gamma shape parameter is defined in different ways, so it might be helpful to include an equation.
The simulation methods state that the negative gamma distribution has a mean of -2.5. Does this apply to 4Ns, and if so, what happens when N changes?
data sets with few polymorphisms, and all multi-allelic sites were excluded. Are the authors confident that this does not introduce biases?
The heatplots would be clearer with scale bars.










