
MAGALHAES Sara
- , CE3C: Centre for Ecology, Evolution and Environmental Changes, Lisboa, Portugal
- Adaptation, Evolutionary Ecology, Experimental Evolution, Reproduction and Sex
- recommender
Recommendations: 3
Reviews: 0
Recommendations: 3
Multi-model inference of non-random mating from an information theoretic approach
Tell me who you mate with, I’ll tell you what’s going on
Recommended by Sara Magalhaes and Alexandre Courtiol based on reviews by Alexandre Courtiol and 2 anonymous reviewersThe study of sexual selection goes as far as Darwin himself. Since then, elaborate theories concerning both intra- and inter-sexual sexual have been developed, and elegant experiments have been designed to test this body of theory. It may thus come as a surprise that the community is still debating on the correct way to measure simple components of sexual selection, such as the Bateman gradient (i.e., the covariance between the number of matings and the number of offspring)[1,2], or to quantify complex behaviours such as mate choice (the non-random choice of individuals with particular characters as mates)[3,4] and their consequences.
One difficulty in the study of sexual selection is evaluating the consequences of non-random mating. Indeed, when non-random mating is observed in a population, it is often difficult to establish whether such mating pattern leads to i) sexual selection per se (selection pressures favouring certain phenotypes), and/or ii) the non-random association of parental genes in their offspring or not. These two processes differ. In particular, assortative (and disassortative) mating can shape genetic covariances without leading to changes in gene frequencies in the population. Their distinction matters because these two processes lead to different evolutionary outcomes, which can have large ripple effects in the evolution of sexual behaviours, sexual ornamentation, and speciation.
In his paper, entitled “Multi-model inference of non-random mating from an information theoretic approach” [5], Carvajal-Rodríguez tackled this issue. The author generated a simple model in which the consequences of non-random mating can be inferred from information on the population frequencies before and after mating. The procedure is as follows: from the initial population frequencies of phenotypes (or genotypes) of both sexes, the model generates predictions on the frequencies after mating, assuming that particular mating patterns have occurred. This leads to different predictions for the phenotypic (or genotypic) frequencies after mating. The particular mating pattern leading to the best fit with the real frequencies is then identified via a model selection procedure (performing model averaging to combine different mating patterns is also possible).
This study builds on a framework introduced by Carvajal-Rodríguez’s colleagues [6] and encompasses later methodological developments involving the author himself [7]. Compared to early work, the new method proposed by the author builds on the relationship between mating pattern and information [8] to distinguish among scenarios that would lead to non-random mating due to different underlying processes, using simple model selection criterion such as the AICc.
The great asset of the proposed method is that it can be applied to the study of natural populations in which the study of mate choice and sexual selection is notoriously difficult. In the manuscript, the procedure is tested on a population of marine gastropods (Littorina saxatilis). This allows the reader to grasp how the method can be applied to a real system. In fact, anyone can try out the method thanks to the freely available software InfoMating programmed by the author. One important assumption underlying the current method is that the frequencies of unmated individuals do not change during the mating season. If this is not the case, the reader may refer to another publication of the same author which relaxes this assumption [9]. These papers are both instrumental for empiricists interested in testing sexual selection theory.
References
[1] Bateman, A. J. (1948). Intra-sexual selection in Drosophila. Heredity, 2(3), 349-368. doi: 10.1038/hdy.1948.21
[2] Jones, A. G. (2009). On the opportunity for sexual selection, the Bateman gradient and the maximum intensity of sexual selection. Evolution: International Journal of Organic Evolution, 63(7), 1673-1684. doi: 10.1111/j.1558-5646.2009.00664.x
[3] Andersson, M., & Simmons, L. W. (2006). Sexual selection and mate choice. Trends in ecology & evolution, 21(6), 296-302. doi: 10.1016/j.tree.2006.03.015
[4] Kuijper, B., Pen, I., & Weissing, F. J. (2012). A guide to sexual selection theory. Annual Review of Ecology, Evolution, and Systematics, 43, 287-311. doi: 10.1146/annurev-ecolsys-110411-160245
[5] Carvajal-Rodríguez, A. (2019). Multi-model inference of non-random mating from an information theoretic approach. bioRxiv, 305730, ver. 5 peer-reviewed and recommended by PCI Evolutionary Biology. doi: 10.1101/305730
[6] Rolán‐Alvarez, E., & Caballero, A. (2000). Estimating sexual selection and sexual isolation effects from mating frequencies. Evolution, 54(1), 30-36. doi: 10.1111/j.0014-3820.2000.tb00004.x
[7] Carvajal-Rodríguez, A., & Rolan-Alvarez, E. (2006). JMATING: a software for the analysis of sexual selection and sexual isolation effects from mating frequency data. BMC Evolutionary Biology, 6(1), 40. doi: 10.1186/1471-2148-6-40
[8] Carvajal-Rodríguez, A. (2018). Non-random mating and information theory. Theoretical population biology, 120, 103-113. doi: 10.1016/j.tpb.2018.01.003
[9] Carvajal-Rodríguez, A. (2019). A generalization of the informational view of non-random mating: Models with variable population frequencies. Theoretical population biology, 125, 67-74. doi: 10.1016/j.tpb.2018.12.004
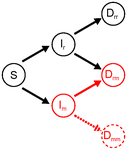
Co-evolution of virulence and immunosuppression in multiple infections
Two parasites, virulence and immunosuppression: how does the whole thing evolve?
Recommended by Sara Magalhaes based on reviews by 2 anonymous reviewersHow parasite virulence evolves is arguably the most important question in both the applied and fundamental study of host-parasite interactions. Typically, this research area has been progressing through the formalization of the problem via mathematical modelling. This is because the question is a complex one, as virulence is both affected and affects several aspects of the host-parasite interaction. Moreover, the evolution of virulence is a problem in which ecology (epidemiology) and evolution (changes in trait values through time) are tightly intertwined, generating what is now known as eco-evolutionary dynamics. Therefore, intuition is not sufficient to address how virulence may evolve.
In their classical model, Anderson and May [1] predict that the optimal virulence level results from a trade-off between increasing parasite load within hosts and promoting transmission between hosts. Although very useful and foundational, this model incurs into several simplifying assumptions. One of the most obvious is that it considers that hosts are infected by a single parasite strain/species. Some subsequent models have thus accounted for multiple infections, generally predicting that this will select for higher virulence, because it increases the strength of selection in the within-host compartment.
Usually, when attacked, hosts deploy defences to combat their parasites. In many systems, however, parasites can suppress the immune response of their hosts. This leads to prolonged infection, which is beneficial for the parasite. However, immunosuppressed hosts are also more prone to infection. Thus, multiple infections are more likely in a population of immunosuppressed hosts, leading to higher virulence, hence a shorter infection period. Thus, the consequences of immunosuppression for the evolution of virulence in a system allowing for multiple infections are not straightforward.
Kamiya et al.[2] embrace this challenge. They create an epidemiological model in which the probability of co-infection trades off with the rate of recovery from infection, via immunosuppression. They then use adaptive dynamics to study how either immunosuppression or virulence evolve in response to one another, to then establish what happens when they both coevolve. They find that when virulence only evolves, its evolutionary equilibrium increases as immunosuppression levels increase. In the reverse case, that is, when virulence is set to a fixed value, the evolutionarily stable immunosuppression varies non-linearly with virulence, with first a decrease, but then an increase at high levels of virulence. The initial decrease of immunosuppression may be due to (a) a decrease in infection duration and/or (b) a decrease in the proportion of double infections, caused by increased levels of virulence. However, as virulence increases, the probability of double infections decreases even in non-immunosuppressed hosts, hence increased immunosuppression is selected for.
The combination of both Evolutionary Stable Strategies (ESSs) yields intermediate levels of virulence and immunosuppression. The authors then address how this co-ESS varies with host mortality and with the shape of the trade-off between the probability of co-infection and the rate of recovery. They find that immunosuppression always decreases with increased host mortality, as it becomes not profitable to invest on this trait. In contrast, virulence peaks at intermediate values of host mortality, unlike the monotonical decrease that is found in absence of immunosuppression. Also, this relationship is predicted to vary with the shape of the trade-off underlying the costs and benefits of immunosuppression.
In sum, Kamiya et al. [2] provide a comprehensive analysis of an important problem in the evolution of host-parasite interactions. The model provides clear predictions, and thus can now be tested using the many systems in which immunosuppression has been detected, provided that the traits that compose the model can be measured.
References
[1] Anderson RM and May RM. 1982. Coevolution of hosts and parasites. Parasitology, 1982. 85: 411–426. doi: 10.1017/S0031182000055360
[2] Kamiya T, Mideo N and Alizon S. 2017. Coevolution of virulence and immunosuppression in multiple infections. bioRxiv, ver. 7 peer-reviewed by PCI Evol Biol, 149211. doi: 10.1101/139147

Evolution of resistance to single and combined floral phytochemicals by a bumble bee parasite
The medicinal value of phytochemicals is hindered by pathogen evolution of resistance
Recommended by Alison Duncan and Sara MagalhaesAs plants cannot run from their enemies, natural selection has favoured the evolution of diverse chemical compounds (phytochemicals) to protect them against herbivores and pathogens. This provides an opportunity for plant feeders to exploit these compounds to combat their own enemies. Indeed, it is widely known that herbivores use such compounds as protection against predators [1]. Recently, this reasoning has been extended to pathogens, and elegant studies have shown that some herbivores feed on phytochemical-containing plants reducing both parasite abundance within hosts [2] and their virulence [3].
Suffering less from parasites is clearly beneficial for infected herbivores. Why then, is this behaviour not fixed in nature? There are, at least, two possible explanations. First, feeding on ‘medicinal’, often toxic, plants may impose costs upon uninfected individuals. Second, parasites may evolve resistance to such chemicals. Whereas the first possibility has been explored, and is taken as evidence for ‘self-medication’ [3], the second hypothesis requires investigation.
A recent study by Palmer-Young et al. [4] fills this gap. This article reports evolution of resistance to two different phytochemicals, alone and in combination, in the trypanosome Crithidia bombi, a bumble bee (Bombus impatiens) parasite. To show this, the authors experimentally evolved a strain of C. bombi in the presence of thymol, eugenol or both simultaneously. These phytochemicals are commonly found in the nectar of several plant species, in particular those of the Lamiaceae, a family containing several aromatic herbs. Prior to selection both phytochemicals reduced C. bombi growth by about 50%. However, C. bombi rapidly evolved resistance in both single and the double phytochemical treatments. Moreover, no cost of resistance was detected when evolved parasites were placed in the ancestral, phytochemical-free environment. Therefore, resistance to phytochemicals would be expected to spread rapidly in natural populations of C. bombi. Clearly, thus, the herbivore strategy of sequestering plant secondary chemical compounds as a defence against their pathogens should fail. The question then is ‘why do they still do it’? Can self-medication work in the longer-term for bumblebees?
Well, yes. The very fact that resistance evolved shows that resistance is not fixed in natural C. bombi populations. This is surprising considering that resistance is not costly. This might be due to a number of reasons. Firstly, there may be costs of resistance that were not detected in this experiment. Second, it may not be possible to evolve universal resistance to the heterogeneity present in the phytochemical environment. Indeed, phytochemical environments are highly varied in time and space and bumblebees will visit different plants presenting different phytochemical cocktails throughout the season. Furthermore, migration of bees from populations exposed to different phytochemicals may prevent the fixation of one resistance type.
Or, it may be self-medication behaviour itself that prevents the evolution of resistance? Indeed, in the same way that infected bees seek cooler temperatures to slow growth of a parasitoid fly [5], they may also seek a more varied diet with diverse phytochemicals to which the parasite cannot evolve, but which reduces parasite growth. Further understanding of arthropod self-medication may thus be instrumental to prevent the observed worldwide decline of pollinators [6]. Furthermore, it may inform on mechanisms that prevent rapid evolution of drug resistance in other systems.
References
[1] Duffey SS. 1980. Sequestration of plant natural products by insects. Annual Review of Entomology 25: 447-477. doi: 10.1146/annurev.en.25.010180.002311
[2] Richardson LL et al. 2015. Secondary metabolites in floral nectar reduce parasite infections in bumblebees. Proceedings of the Royal Society of London B 282: 20142471. doi: 10.1098/rspb.2014.2471
[3] Lefèvre T et al. 2010. Evidence for trans-generational medication in nature. Ecology Letters 13: 1485-93. doi: 10.1111/j.1461-0248.2010.01537.x
[4] Palmer-Young EC, Sadd BM, Adler LS. 2017. Evolution of resistance to single and combined floral phytochemicals by a bumble bee parasite. Journal of Evolutionary Biology 30: 300-312. doi: 10.1111/jeb.13002
[5] Müller CB, Schmid-Hempel P. 1993. Exploitation of cold temperature as defence against parasitoids in bumblebees. Nature 363: 65-67. doi: 10.1038/363065a0
[6] Potts SG et al. 2010. Global pollinator declines: trends, impacts and drivers. Trends in Ecology and Evolution 25: 345-353. doi: 10.1016/j.tree.2010.01.007