The evolutionary response of populations to changing or novel environments is a topic that unites the interests of evolutionary biologists, ecologists, and biomedical researchers [1]. A prominent phenomenon in this research area is evolutionary rescue, whereby a population that is otherwise doomed to extinction survives due to the spread of new or pre-existing mutations that are beneficial in the new environment. Scenarios of evolutionary rescue require a specific set of parameters: the absolute growth rate has to be negative before the rescue mechanism spreads, upon which the growth rate becomes positive. However, potential examples of its relevance exist (e.g., [2]). From a theoretical point of view, the technical challenge but also the beauty of evolutionary rescue models is that they combine the study of population dynamics (i.e., changes in the size of populations) and population genetics (i.e., changes in the frequencies in the population). Together, the potential relevance of evolutionary rescue in nature and the models' theoretical appeal has resulted in a suite of modeling studies on the subject in recent years.
In this manuscript [3], Tomasini and Peischl address a question that has been contentiously discussed in the literature: when does migration favor evolutionary rescue? They expand on past work (specifically, [4, 5]) by studying the influence of the interaction of the speed and severity of environmental change and the amount of dispersal on the probability of evolutionary rescue. They develop simple analytical results (complemented by simulations) for a haploid one-locus model of two populations connected by gene flow, where both populations deteriorate successively such that evolutionary rescue is required for the metapopulation to survive. For example, the authors derive a simple analytical condition demonstrating that migration between the subpopulations favors evolutionary rescue if environmental change occurs slowly across the two populations (which leaves time for the second population to serve as an immigration source), if the new environment is very harsh and/or if rescue mutations are strongly beneficial in the new environment. The latter conditions ensure that the rescue mutations can spread easily in the new environment without much competition with immigrating, maladapted, genotypes. This result is intuitive and connects between traditional single and multiple-deme models.
Altogether, Tomasini and Peischl present an extensive theoretical study and address also the effect of various tweaks to the model assumptions, such as asymmetries in gene flow and/or carrying capacities, and the effects of different density regulation and local growth rates. They successfully made an effort to explain and interpret their results for a general audience, such that also non-theoreticians should not be afraid to take a look at this manuscript.

References

[1] Bell, G. (2017). Evolutionary Rescue. Annual Review of Ecology, Evolution, and Systematics 48(1), 605-627. doi: 10.1146/annurev-ecolsys-110316-023011
[2] Oziolor, E. M., Reid, N. M., Yair, S. et al. (2019). Adaptive introgression enables evolutionary rescue from extreme environmental pollution. Science, 364(6439), 455-457. doi: 10.1126/science.aav4155
[3] Tomasini, M. and Peischl, S. (2020) When does gene flow facilitate evolutionary rescue? bioRxiv, 622142, ver. 5 peer-reviewed and recommended by PCI Evolutionary Biology. doi: 10.1101/622142
[4] Uecker, H., Otto, S. P., and Hermisson, J. (2014). Evolutionary rescue in structured populations. The American Naturalist, 183(1), E17-E35. doi: 10.1086/673914
[5] Tomasini, M., and Peischl, S. (2018). Establishment of locally adapted mutations under divergent selection. Genetics, 209(3), 885-895. doi: 10.1534/genetics.118.301104

The increase in the prevalence of (antibiotic) resistance has become a major global health concern and is an excellent example of the impact of real-time evolution on human society. This has led to a boom of studies that investigate the mechanisms and factors involved in the evolution of resistance, and to the spread of the concept of "costs of resistance". This concept refers to the relative fitness disadvantage of a drug-resistant genotype compared to a non-resistant reference genotype in the ancestral (untreated) environment.

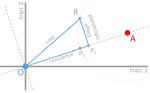
In their paper, Lenormand et al. [1] discuss the history of this concept and highlight its caveats and limitations. The authors address both practical and theoretical problems that arise from the simplistic view of "costly resistance" and argue that they can be prejudicial for antibiotic resistance studies. For a better understanding, they visualize their points of critique by means of Fisher's Geometric model.

The authors give an interesting historical overview of how the concept arose and speculate that it emerged (during the 1980s) in an attempt by ecologists to spread awareness that fitness can be environment-dependent, and because of the concept's parallels to trade-offs in life-history evolution. They then identify several problems that arise from the concept, which, besides the conceptual misunderstandings that they can cause, are important to keep in mind when designing experimental studies.

The authors highlight and explain the following points:
1. Costs of resistance do not necessarily imply pleiotropic effects of a resistance mutation, and pleiotropy is not necessarily the cause of fitness trade-offs.
2. Any non-treated environment and any treatment dose can result in a different cost.
3. Different reference genotypes may result in different costs. Specifically, the reference genotype has to be "optimally" adapted to the reference environment to provide an accurate measurement of costs.

Lenormand et al.'s paper [1] is a timely perspective piece in light of the ever-increasing efforts to understand and tackle resistance evolution [2]. Although some readers may shy away from the rather theoretical presentation of the different points of concern, it will be useful for both theoretical and empirical readers by illustrating the misconceptions that can arise from the concept of the cost of resistance. Ultimately, the main lesson to be learned from this paper may not be to ban the term "cost of resistance" from one's vocabulary, but rather to realize that the successful fight against drug resistance requires more differential information than the measurement of fitness effects in a drug-treated vs. non-treated environment in the lab [3-4]. Specifically, a better integration of the ecological aspects of drug resistance evolution and maintenance is needed [5], and we are far from a general understanding of how environmental factors interact and influence an organism's (absolute and relative) fitness and the effect of resistance mutations.

References

[1] Lenormand T, Harmand N, Gallet R. 2018. Cost of resistance: an unreasonably expensive concept. bioRxiv 276675, ver. 3 peer-reviewed by Peer Community In Evolutionary Biology. doi: 10.1101/276675
[2] Andersson DI and Hughes D. Persistence of antibiotic resistance in bacterial populations. 2011. FEMS Microbiology Reviews, 35: 901-911. doi: 10.1111/j.1574-6976.2011.00289.x
[3] Chevereau G, Dravecká M, Batur T, Guvenek A, Ayhan DH, Toprak E, Bollenbach T. 2015. Quantifying the determinants of evolutionary dynamics leading to drug resistance. PLoS biology 13, e1002299. doi: 10.1371/journal.pbio.1002299
[4] Bengtsson-Palme J, Kristiansson E, Larsson DGJ. 2018. Environmental factors influencing the development and spread of antibiotic resistance. FEMS Microbiology Reviews 42: 68–80. doi: 10.1093/femsre/fux053
[5] Hiltunen T, Virta M, Laine AL. 2017. Antibiotic resistance in the wild: an eco-evolutionary perspective. Philosophical Transactions of the Royal Society B: Biological Sciences 372: 20160039. doi: 10.1098/rstb.2016.0039

The increasing number of reported cases of antibiotic resistance is one of today’s major public health concerns. Dealing with this threat involves understanding what drives the evolution of antibiotic resistance and investigating whether we can predict (and subsequently avoid or circumvent) it [1].
One of the most illustrative and common models of adaptation (and, hence, resistance evolution) is Fisher’s Geometric Model (FGM). The original model maps phenotypes to fitness, meaning that each point in the fitness landscape corresponds to a phenotype rather than a genotype. However, it has been shown that when mutations are numerous enough, FGM can also describe adaptive walks in genotype space [2]. Nevertheless, limitations have been highlighted, particularly when trying to study complex scenarios such as antibiotic resistance evolution [3].
Harmand et al. [4] incorporated three extensions to the FGM, which allowed them to match the mutational patterns of antibiotic resistance that they obtained from a screen across a gradient of drug concentrations. The implemented extensions took into account that: 1) only a subset of mutations may contribute to traits under selection, reflecting that not all regions in the genome affect the ability to resist antibiotics; 2) mutations that confer a fitness increase in one environment may not reflect a similar increase in others, if the selective constraints are different; and 3) different antibiotic concentrations may either constrain the maximum fitness that populations can reach (changing the height of the fitness peak) or change the rate of fitness increase with each mutation (changing the width/slope of the peak).
Traditionally, most empirical fitness landscape studies have focused on a subset of mutations obtained after laboratory evolution in specific conditions [5, 6]. The results obtained in Harmand et al. [4] indicate a potential shortcoming of studying these small fitness landscapes: rather than having a constrained evolutionary path to a resistant phenotype, as previously observed, their results suggest that antibiotic resistance can be the product of mutations in different regions of the genome. Returning to the fitness landscape perspective, this indicates that there are many alternative paths that can lead to the evolution of antibiotic resistance. This comparison points at a difficult challenge when aiming at developing a predictive framework for evolution: real-time experiments may indicate that evolution is likely to take similar and predictable paths because the strongest and most frequent mutations dictate the outcome, whereas systematic screens of mutants potentially indicate several paths, that may, however, not be relevant in nature. Only a combination of different experimental approaches with motivated theory as presented in Harmand et al. [4] will allow for a better understanding of where in this continuum evolution is taking place in nature, and to which degree we are able to interfere with it in order to slow down adaptation.

References

[1] Palmer AC, and Kishony R. 2013. Understanding, predicting and manipulating the genotypic evolution of antibiotic resistance. Nature Review Genetics 14: 243—248. doi: 10.1038/nrg3351

[2] Tenaillon O. 2014. The utility of Fisher’s geometric model in evolutionary genetics. Annual Review of Ecology, Evolution and Systematics 45: 179—201. doi: 10.1146/annurev-ecolsys-120213-091846

[3] Blanquart F and Bataillon T. 2016. Epistasis and the structure of fitness landscapes: are experimental fitness landscapes compatible with Fisher’s geometric model? Genetics 203: 847—862. doi: 10.1534/genetics.115.182691

[4] Harmand N, Gallet R, Jabbour-Zahab R, Martin G and Lenormand T. 2017. Fisher’s geometrical model and the mutational patterns of antibiotic resistance across dose gradients. Evolution 71: 23—37. doi: 10.1111/evo.13111

[5] de Visser, JAGM, and Krug J. 2014. Empirical fitness landscapes and the predictability of evolution. Nature 15: 480—490. doi: 10.1038/nrg3744

[6] Palmer AC, Toprak E, Baym M, Kim S, Veres A, Bershtein S and Kishony R. 2015. Delayed commitment to evolutionary fate in antibiotic resistance fitness landscapes. Nature Communications 6: 1—8. doi: 10.1038/ncomms8385