MULLON Charles
- Department of Ecology and Evolution, University of Lausanne, Lausanne, Switzerland
- Evolutionary Dynamics, Evolutionary Theory
- recommender
Recommendations: 3
Review: 1
Recommendations: 3
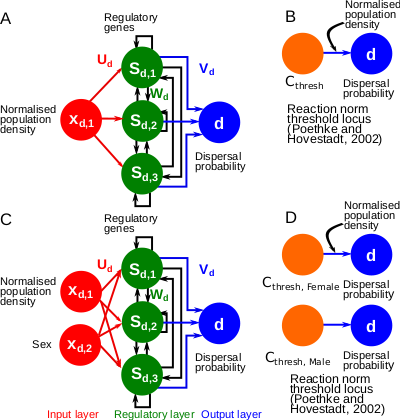
A gene-regulatory network model for density-dependent and sex-biased dispersal evolution during range expansions
Evolved gene-regulatory networks underlying dispersal plasticity can accelerate range expansions
Recommended by Charles Mullon based on reviews by Arnaud Le Rouzic and 2 anonymous reviewers
The genetic architecture of local adaptation in a cline
Environmental and fitness landscapes matter for the genetic basis of local adaptation
Recommended by Charles Mullon based on reviews by 2 anonymous reviewersNatural landscapes are often composite, with spatial variation in environmental factors being the norm rather than exception. Adaptation to such variation is a major driver of diversity at all levels of biological organization, from genes to phenotypes, species and ultimately ecosystems. While natural selection favours traits that show a better fit to local conditions, the genomic response to such selection is not necessarily straightforward. This is because many quantitative traits are complex and the product of many loci, each with a small to moderate phenotypic contribution. Adapting to environmental challenges that occur in narrow ranges may thus prove difficult as each individual locus is easily swamped by alleles favoured across the rest of the population range.
To better understand whether and how evolution overcomes such a hurdle, Laroche and Lenormand [1] combine quantitative genetics and population genetic modelling to track genomic changes that underpin a trait whose fitness optimum differs between a certain spatial range, referred to as a “pocket”, and the rest of the habitat. As it turns out from their analysis, one critical and probably underappreciated factor in determining the type of genetic architecture that evolves is how fitness declines away from phenotypic optima. One classical and popular model of fitness landscape that relates trait value to reproductive success is Gaussian, whereby small trait variations away from the optimum result in even smaller variations in fitness. This facilitates local adaptation via the invasion of alleles of small effects as carriers inside the pocket show a better fit while those outside the pocket only suffer a weak fitness cost. By contrast, when the fitness landscape is more peaked around the optimum, for instance where the decline is linear, adaptation through weak effect alleles is less likely, requiring larger pockets that are less easily swamped by alleles selected in the rest of the range.
In addition to mathematically investigating the initial emergence of local adaptation, Laroche and Lenormand use computer simulations to look at its long-term maintenance. In principle, selection should favour a genetic architecture that consolidates the phenotype and increases its heritability, for instance by grouping several alleles of large effects close to one another on a chromosome to avoid being broken down by meiotic recombination. Whether or not this occurs also depends on the fitness landscape. When the landscape is Gaussian, the genetic architecture of the trait eventually consists of tightly linked alleles of large effects. The replacement of small effects by large effects loci is here again promoted by the slow fitness decline around the optimum. This is because any shift in architecture in an adapted population requires initially crossing a fitness valley. With a Gaussian landscape, this valley is shallow enough to be crossed, facilitated by a bit of genetic drift. By contrast, when fitness declines linearly around the optimum, genetic architecture is much less evolutionarily labile as any architecture change initially entails a fitness cost that is too high to bear.
Overall, Laroche and Lenormand provide a careful and thought-provoking analysis of a classical problem in population genetics. In addition to questioning some longstanding modelling assumptions, their results may help understand why differentiated populations are sometimes characterized by “genomic islands” of divergence, and sometimes not.
References
[1] Laroche F, Lenormand T (2022) The genetic architecture of local adaptation in a cline. bioRxiv, 2022.06.30.498280, ver. 4 peer-reviewed and recommended by Peer Community in Evolutionary Biology. https://doi.org/10.1101/2022.06.30.498280

Evolution and genetic architecture of disassortative mating at a locus under heterozygote advantage
Evolutionary insights into disassortative mating and its association to an ecologically relevant supergene
Recommended by Charles Mullon based on reviews by Tom Van Dooren and 2 anonymous reviewers*Heliconius* butterflies are famous for their colorful wing patterns acting as a warning of their chemical defenses [1]. Most species are involved in Müllerian mimicry assemblies, as predators learn to associate common wing patterns with unpalatability and preferentially target rare variants. Such positive-frequency dependent selection homogenizes wing patterns at different localities, and in several species, all individuals within a community belong to the same morph [2]. In this respect, *H. numata* stands out. This species shows stable local polymorphism across multiple localities, with local populations home to up to seven distinct morphs [2]. Although a balance between migration and local positive-frequency dependent selection can allow some degree of local polymorphism, theory suggests that this occurs only when migration is within a narrow window [3]. One factor that potentially enhances local polymorphism in *H. numata* is disassortative mating. Mate choice assays have in fact revealed that females of this species tend to reject males with the same wing pattern [4]. However the evolution of such mating behavior and its effect on polymorphism remain unclear when selection is locally positive-frequency dependent. Using a mathematical model, Maisonneuve *et al.* [5] clarify the conditions that favor the evolution of disassortative mating in the complicated system of *H. numata*. In particular, they investigate whether the genetic basis of wing colour can favor the emergence of disassortative mating. Variation in wing pattern in *H. numata* is controlled by the supergene P, which is a single genomic region harboring multiple protein coding genes that have ceased to recombine due to chromosomal inversions [6]. If such remarkable genetic configuration allows for the co-adaptation of multiple loci participating to a complex phenotype such as wing color pattern, the absence of recombination can also result in the accumulation of deleterious mutations [7]. In fact, alleles at the P locus have been associated with a recessive genetic load, leading to a fitness advantage for heterozygotes at this locus [8]. Can this fitness advantage to heterozygotes lead to the evolution of disassortative mating? And if so, can such evolution lead to the maintenance of local polymorphism in spite of strong positive frequency-dependent selection? To investigate these questions, Maisonneuve *et al.* [5] model evolution at two loci, one is the P locus for wing pattern, and the other influences mating behavior. The population is divided among two connected patches that differ in their butterfly communities, so that different alleles at the P locus are favored by positive frequency-dependent selection in different patches. The different alleles at the P locus are ordered in dominance relationships such that the most dominant over wing color pattern are also those with the highest load. By tracking the dynamics of haplotype frequencies in the population, the authors first show that disassortative mating readily evolves via the invasion of an allele causing females carrying it to reject males that resemble them phenotypically. Such “self-referencing” mechanism of mate choice, however, has never been reported and has been argued to be rare due to its complicated nature [9]. Maisonneuve *et al.* [5] then compare the evolution of disassortative mating via two alternative mechanisms: attraction and rejection. In these cases, alleles at the mating locus determine attraction to or rejection of specific phenotypes (e.g., under attraction rule, allele “B” encodes attraction to males with phenotype B). With the P and mating loci fully linked, disassortative mating can evolve under all three mechanisms (self-referencing, attraction and rejection), but tends to be less prevalent at equilibrium under attraction rule. This in turn results in the maintenance of less genetic variation under attraction compared to the other mating mechanisms. The loss of variation that occurs under attraction rules is due to a combination of dominance relationships between alleles at the P locus and the searching cost to females in finding rare types of males. When a particular wing pattern, say B, is only expressed in homozygotic form, B males are relatively rare. Females that carry the allele at the mating locus causing them to be attracted to such males then suffer a fitness cost due to lost mating opportunities. This mating allele is therefore purged, and in turn so is the recessive allele for B phenotype at the P locus. Under self-referencing and rejection rules, however, choosy females only reject males of a specific phenotype. They can therefore potentially mate with larger pool of males than females attracted to a single type. As a result, self-referencing and rejection rules are less sensitive to demographic effects and so are more conducive to disassortative mating evolution. In their final analysis, Maisonneuve *et al.* [5] investigate the influence of recombination among the P and mating loci. They show that recombination has different effects on disassortative mating evolution depending on the mechanism of mate choice. Under the self-referencing rule, loose linkage leads to higher levels of disassortative mating and polymorphism than when linkage is tight. Under attraction or rejection rule, however, even very limited recombination completely inhibits the evolution of disassortative mating. This is because, with alleles at the mating locus coding for attraction/rejection to specific males, recombination breaks the association between the P and mating loci necessary for disassortative mating. By contrast, disassortative mating via a self-referencing rule does not depend on the linkage among the P and mating loci: females choose males that are different to themselves independently from the alleles they carry at the P locus. Taken together, Maisonneuve *et al.*’s analyses [5] show that disassortative mating can readily evolve in a system like *H. numata*, but that this evolution depends on the genetic architecture of mating behavior. The architectures that are more conducive to the evolution of disassortative mating are: (1) epistatic interactions among the P and mating loci such that females are able to recognize their own phenotype and base their mating decision upon this information (self-referencing rule); and (2) full linkage among the P supergene and a mating locus that triggers rejection of a specific color pattern. While the mechanisms behind disassortative mating remain to be elucidated, assortative mating seems to rely on alleles triggering attraction to specific cues with variation in attraction and cues linked together [10]. These observations support the notion that disassortative mating is due to alleles causing rejection, in tight linkage to the P locus. If so, mating loci would in fact be part of the P supergene, thus controlling not only intricate wing color pattern but also mating behavior. Beyond the specific system of *H. numata*, Maisonneuve *et al.*’s study [5] helps understand the evolution of disassortative mating and its association with the genetic architecture of correlated traits. In particular, Maisonneuve *et al.* [5] expands the role of supergenes for ecologically relevant traits to mating behavior, further bolstering the relevance of these remarkable genetic elements in the maintenance of variation in complex and elaborate phenotypes. **References** [1] Merrill, R M, K K Dasmahapatra, J W Davey, D D Dell'Aglio, J J Hanly, B Huber, C D Jiggins, et al. (2015). The Diversification of Heliconius butterflies: What Have We Learned in 150 Years? Journal of Evolutionary Biology 28 (8), 1417–38. [https://doi.org/10.1111/jeb.12672.](https://doi.org/10.1111/jeb.12672.) [2] Joron M, IR Wynne, G Lamas, and J Mallet (1999). Variable selection and the coexistence of multiple mimetic forms of the butterfly Heliconius numata. Evolutionary Ecology 13, 721– 754. [https://doi.org/10.1023/A:1010875213123](https://doi.org/10.1023/A:1010875213123) [3] Joron M and Y Iwasa (2005). The evolution of a Müllerian mimic in a spatially distributed community. Journal of Theoretical Biology 237, 87–103. [https://doi.org/10.1016/j.jtbi.2005.04.005](https://doi.org/10.1016/j.jtbi.2005.04.005) [4] Chouteau M, V Llaurens, F Piron-Prunier, and M Joron (2017). Polymorphism at a mimicry su- pergene maintained by opposing frequency-dependent selection pressures. Proceedings of the National Academy of Sciences 114, 8325–8329. [https://doi.org/10.1073/pnas.1702482114](https://doi.org/10.1073/pnas.1702482114) [5] Maisonneuve, L, Chouteau, M, Joron, M and Llaurens, V. (2020). Evolution and genetic architecture of disassortative mating at a locus under heterozygote advantage. bioRxiv, 616409, ver. 9 peer-reviewed and recommended by PCI Evolutionary Biology. [https://doi.org/10.1101/616409](https://doi.org/10.1101/616409) [6] Joron M, L Frezal, RT Jones, NL Chamberlain, SF Lee, CR Haag, A Whibley, M Becuwe, SW Baxter, L Ferguson, et al. (2011). Chromosomal rearrangements maintain a polymorphic super- gene controlling butterfly mimicry. Nature 477, 203. [https://doi.org/10.1038/nature10341](https://doi.org/10.1038/nature10341) [7] Schwander T, R Libbrecht, and L Keller (2014). Supergenes and Complex Phenotypes.” Current Biology. 24 (7), 288–94. [https://doi.org/10.1016/j.cub.2014.01.056.](https://doi.org/10.1016/j.cub.2014.01.056.) [8] Jay P, M Chouteau, A Whibley, H Bastide, V Llaurens, H Parrinello, and M Joron (2019). Mutation accumulation in chromosomal inversions maintains wing pattern polymorphism in a butterfly. bioRxiv. [https://doi.org/ 10.1101/736504. ](https://doi.org/ 10.1101/736504. ) [9] Kopp M, MR Servedio, TC Mendelson, RJ Safran, RL Rodrıguez, ME Hauber, EC Scordato, LB Symes, CN Balakrishnan, DM Zonana, et al. (2018). Mechanisms of assortative mating in speciation with gene flow: connecting theory and empirical research. The American Naturalist 191, 1–20. [https://doi.org/10.1086/694889](https://doi.org/10.1086/694889) [10] Merrill RM, P Rastas, SH Martin, MC Melo, S Barker, J Davey, WO McMillan, and CD Jiggins (2019). Genetic dissection of assortative mating behavior. PLoS biology 17, e2005902. [https://doi.org/10.1371/journal.pbio.2005902](https://doi.org/10.1371/journal.pbio.2005902)
Review: 1

Gene network robustness as a multivariate character
Genetic and environmental robustness are distinct yet correlated evolvable traits in a gene network
Recommended by Frédéric Guillaume based on reviews by Diogo Melo, Charles Mullon and Charles RocabertOrganisms often show robustness to genetic or environmental perturbations. Whether these two components of robustness can evolve separately is the focus of the paper by Le Rouzic [1]. Using theoretical analysis and individual-based computer simulations of a gene regulatory network model, he shows that multiple aspects of robustness can be investigated as a set of pleiotropically linked quantitative traits. While genetically correlated, various robustness components (e.g., mutational, developmental, homeostasis) of gene expression in the regulatory network evolved more or less independently from each other under directional selection. The quantitative approach of Le Rouzic could explain both how unselected robustness components can respond to selection on other components and why various robustness-related features seem to have their own evolutionary history. Moreover, he shows that all components were evolvable, but not all to the same extent. Robustness to environmental disturbances and gene expression stability showed the largest responses while increased robustness to genetic disturbances was slower. Interestingly, all components were positively correlated and remained so after selection for increased or decreased robustness.
This study is an important contribution to the discussion of the evolution of robustness in biological systems. While it has long been recognized that organisms possess the ability to buffer genetic and environmental perturbations to maintain homeostasis (e.g., canalization [2]), the genetic basis and evolutionary routes to robustness and canalization are still not well understood. Models of regulatory gene networks have often been used to address aspects of robustness evolution (e.g., [3]). Le Rouzic [1] used a gene regulatory network model derived from Wagner’s model [4]. The model has as end product the expression level of a set of genes influenced by a set of regulatory elements (e.g., transcription factors). The level and stability of expression are a property of the regulatory interactions in the network.
Le Rouzic made an important contribution to the study of such gene regulation models by using a quantitative genetics approach to the evolution of robustness. He crafted a way to assess the mutational variability and selection response of the components of robustness he was interested in. Le Rouzic’s approach opens avenues to investigate further aspects of gene network evolutionary properties, for instance to understand the evolution of phenotypic plasticity.
Le Rouzic also discusses ways to measure his different robustness components in empirical studies. As the model is about gene expression levels at a set of protein-coding genes influenced by a set of regulatory elements, it naturally points to the possibility of using RNA sequencing to measure the variation of gene expression in know gene networks and assess their robustness. Robustness could then be studied as a multidimensional quantitative trait in an experimental setting.
References
[1] Le Rouzic, A (2022) Gene network robustness as a multivariate character. arXiv: 2101.01564, ver. 5 peer-reviewed and recommended by Peer Community in Evolutionary Biology. https://arxiv.org/abs/2101.01564
[2] Waddington CH (1942) Canalization of Development and the Inheritance of Acquired Characters. Nature, 150, 563–565. https://doi.org/10.1038/150563a0
[3] Draghi J, Whitlock M (2015) Robustness to noise in gene expression evolves despite epistatic constraints in a model of gene networks. Evolution, 69, 2345–2358. https://doi.org/10.1111/evo.12732
[4] Wagner A (1994) Evolution of gene networks by gene duplications: a mathematical model and its implications on genome organization. Proceedings of the National Academy of Sciences, 91, 4387–4391. https://doi.org/10.1073/pnas.91.10.4387