
GUILLAUME Frédéric
- Organismal and Evolutionary Biology Research Programme, University of Helsinki, Helsinki, Finland
- Adaptation, Bioinformatics & Computational Biology, Evolutionary Dynamics, Evolutionary Theory, Experimental Evolution, Genotype-Phenotype, Phenotypic Plasticity, Population Genetics / Genomics, Quantitative Genetics
- recommender
Recommendations: 4
Reviews: 3
Recommendations: 4
On the potential for GWAS with phenotypic population means and allele-frequency data (popGWAS)
popGWAS: Data-efficient trait mapping in natural populations for biodiversity research
Recommended by Frédéric Guillaume based on reviews by Petri Kemppainen and 1 anonymous reviewerThe study by Pfenninger (2025) addresses the critical need to understand the genomic basis of ecologically important traits to better predict and respond to the impacts of global change on biodiversity (Gienapp et al. 2017). It introduces the popGWAS, a novel GWAS approach, which utilizes phenotypic population means and genome-wide allele frequency data, obtainable through methods like Pool-sequencing (Pool-Seq), to identify the genetic loci underlying quantitative polygenic traits in natural populations and predict their mean. The core idea is that trait-increasing alleles should exhibit higher frequencies in populations with higher mean trait values. popGWAS then maps mean allele frequencies across populations to their trait means. Working with as many allele frequency values as populations sampled, popGWAS potentially has more power to find significant associations at genomic loci than individual-based GWAS working with three genotypes at a locus. This new method addresses some of the problems faced by traditional genome-wide association studies (GWAS), which require extensive resources and large sample sizes, posing challenges for biodiversity research on non-model species in natural populations.
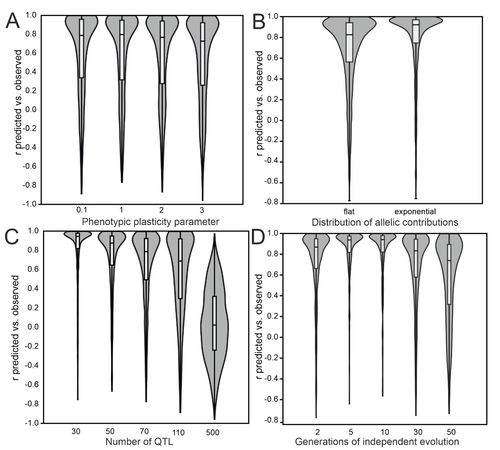
To evaluate the effectiveness of popGWAS, Pfenninger (2025) conducted extensive population genetic forward simulations, examining scenarios with varying numbers of populations, ranging from 12 to 60. The results indicated that popGWAS performance improved with increasing sample size, showing a diminishing return above 36 populations. In a direct comparison across all simulation scenarios, popGWAS consistently outperformed individual-based GWAS (iGWAS). On average, popGWAS identified more true positive loci than iGWAS. In addition, when combined with minimum entropy feature selection (MEFS), popGWAS achieved large predictive accuracy of population means of 0.8 or better in over 97% of simulations with 36 or more populations, regardless of other parameters. In contrast, iGWAS failed to generate valid phenotypic predictions in over 70% of the simulations. Also, unlike iGWAS, popGWAS did not suffer from p-value inflation. Yet, population structure or varying levels of relatedness among individuals were not fully accounted for in the simulations. The extent to which popGWAS would be sensitive to such individual covariates remains to be shown. Finally, popGWAS was relatively insensitive to low trait heritability because random individual variation gets averaged out when calculating the population mean trait value.
The study demonstrates that popGWAS is a promising approach, particularly for oligogenic and moderately polygenic traits. The method performs more poorly for polygenic traits with large genetic redundancy, where different alleles contribute to the same trait mean in different populations. The method thus performs better when large-effect loci contribute to genetic differentiation in parallel across populations, as expected when gene flow is moderate to high (Yeaman & Whitlock 2011). Low genomic predictability is reached when drift dominates or when genetic architectures are highly polygenic.
The popGWAS method proved effective with a moderate number of sampled populations and, when combined with machine learning for genomic prediction, exhibited strong performance in predicting population means, even for low-heritability traits. Notably, popGWAS consistently outperformed iGWAS in terms of identifying true positive loci and prediction accuracy. This suggests that popGWAS can make GWAS studies more accessible for biodiversity genomics research, providing a valuable tool for dissecting the genetic basis of complex traits in natural populations. A key aspect contributing to the efficiency of popGWAS is its compatibility with pooled sequencing (Pool-Seq). Pool-Seq provides estimates of allele frequencies within a population by sequencing a mixed DNA sample representing multiple individuals from that population (Futschik & Schlötterer 2010). This approach is significantly more cost-effective than sequencing each individual separately, allowing researchers to obtain genome-wide allele frequency data across multiple populations with a substantially reduced budget. This data efficiency makes GWAS more accessible to a wider range of researchers, particularly those working in biodiversity genomics where financial resources may be limited. Furthermore, popGWAS can be coupled with bulk phenotyping methods, such as automatic video recording, remote sensing, metabolomics/transcriptomics, etc., to efficiently obtain population-level phenotypic data, further streamlining the research process. Ultimately, popGWAS represents a valuable addition to the geneticist's toolkit, offering a complementary approach to iGWAS that can be particularly advantageous in specific research contexts where predicting trait mean is more important than resolving the precise genetic basis of a trait.
References
Futschik, A. and Schlötterer, C. 2010. The Next Generation of Molecular Markers From Massively Parallel Sequencing of Pooled DNA Samples. Genetics 186(1): 207-218. https://doi.org/10.1534/genetics.110.114397
Gienapp, P., Fior, S., Guillaume, F., Lasky, J. R., Sork, V. L. and Csilléry, K. 2017. Genomic Quantitative Genetics to Study Evolution in the Wild. Trends Ecol. Evol. 32(12): 897-908. https://doi.org/10.1016/j.tree.2017.09.004
Markus Pfenninger (2025) On the potential for GWAS with phenotypic population means and allele-frequency data (popGWAS). bioRxiv, ver.3 peer-reviewed and recommended by PCI Evol Biol https://doi.org/10.1101/2024.06.12.598621
Yeaman, S. and Whitlock, M. C. 2011. The genetic architecture of adaptation under migration-selection balance. Evolution 65(7): 1897-1911. https://doi.org/10.1111/j.1558-5646.2011.01269.x
Phenotypic stasis with genetic divergence
Phenotypic stasis despite genetic divergence and differentiation in Caenorhabditis elegans.
Recommended by Frédéric Guillaume based on reviews by Benoit Pujol and Pedro SimõesExplaining long periods of evolutionary stasis, the absence of change in trait means over geological times, despite the existence of abundant genetic variation in most traits has challenged evolutionary theory since Darwin's theory of evolution by gradual modification (Estes & Arnold 2007). Stasis observed in contemporary populations is even more daunting since ample genetic variation is usually coupled with the detection of selection differentials (Kruuk et al. 2002, Morrissey et al. 2010). Moreover, rapid adaptation to environmental changes in contemporary populations, fuelled by standing genetic variation provides evidence that populations can quickly respond to an adaptive challenge. Explanations for evolutionary stasis usually invoke stabilizing selection as a main actor, whereby optimal trait values remain roughly constant over long periods of time despite small-scale environmental fluctuations. Genetic correlation among traits may also play a significant role in constraining evolutionary changes over long timescales (Schluter 1996). Yet, genetic constraints are rarely so strong as to completely annihilate genetic changes, and they may evolve. Patterns of genetic correlations among traits, as captured in estimates of the G-matrix of additive genetic co-variation, are subject to changes over generations under the action of drift, migration, or selection, among other causes (Arnold et al. 2008). Therefore, under the assumption of stabilizing selection on a set of traits, phenotypic stasis and genetic divergence in patterns of trait correlations may both be observed when selection on trait correlations is weak relative to its effect on trait means.
Mallard et al. (2023) set out to test whether selection or drift may explain the divergence in genetic correlation among traits in experimental lines of the nematode Caenorhabditis elegans and whether stabilizing selection may be a driver of phenotypic stasis. To do so, they analyzed the evolution of locomotion behavior traits over 100 generations of lab evolution in a constant and homogeneous environment after 140 generations of domestication from a largely differentiated set of founder populations. The locomotion traits were transition rates between movement states and direction (still, forward or backward movement). They could estimate the traits' broad-sense G-matrix in three populations at two generations (50 and 100), and in the ancestral mixed population. Similarly, they estimated the shape of the selection surface by regressing locomotion behavior on fertility. Armed with both G-matrix and surface estimates, they could test whether the G's orientation matched selection's orientation and whether changes in G were constrained by selection. They found stasis in trait mean over 100 generations but divergence in the amount and orientation of the genetic variation of the traits relative to the ancestral population. The selected populations changed orientation of their G-matrices and lost genetic variation during the experiment in agreement with a model of genetic drift on quantitative traits. Their estimates of selection also point to mostly stabilizing selection on trait combinations with weak evidence of disruptive selection, suggesting a saddle-shaped selection surface. The evolutionary responses of the experimental populations were mostly consistent with small differentiation in the shape of G-matrices during the 100 generations of stabilizing selection.
Mallard et al. (2023) conclude that phenotypic stasis was maintained by stabilizing selection and drift in their experiment. They argue that their findings are consistent with a "table-top mountain" model of stabilizing selection, whereby the population is allowed some wiggle room around the trait optimum, leaving space for random fluctuations of trait variation, and especially trait co-variation. The model is an interesting solution that might explain how stasis can be maintained over contemporary times while allowing for random differentiation of trait genetic co-variation. Whether such differentiation can then lead to future evolutionary divergence once replicated populations adapt to a new environment is an interesting idea to follow.
References
Arnold, S. J., Bürger, R., Hohenlohe, P. A., Ajie, B. C. and Jones, A. G. 2008. Understanding the evolution and stability of the G-matrix. Evolution 62(10): 2451-2461.
https://doi.org/10.1111/j.1558-5646.2008.00472.x
Estes, S. and Arnold, S. J. 2007. Resolving the Paradox of Stasis: Models with Stabilizing Selection Explain Evolutionary Divergence on All Timescales.. Am. Nat. 169(2): 227-244.
https://doi.org/10.1086/510633
Kruuk, L. E. B., Slate, J., Pemberton, J. M., Brotherstone, S., Guinness, F. and Clutton-Brock, T. 2002. Antler size in red deer: Heritability and selection but no evolution. Evolution 56(8): 1683-1695.
https://doi.org/10.1111/j.0014-3820.2002.tb01480.x
Mallard, F., Noble, L., Guzella, T., Afonso, B., Baer, C. F., Teotónio, H. 2023. Phenotypic stasis with genetic divergence. bioRxiv, ver. 3 peer-reviewed and recommended by Peer Community in Evolutionary Biology.
https://doi.org/10.1101/2022.05.28.493856
Morrissey, M. B., Kruuk, L. E. B. and Wilson, A. J. 2010. The danger of applying the breeder's equation in observational studies of natural populations. J Evolution Biol 23(11): 2277-2288.
https://doi.org/10.1111/j.1420-9101.2010.02084.x
Schluter, D. 1996. Adaptive radiation along genetic lines of least resistance. Evolution 50(5): 1766-1774.
https://doi.org/10.1111/j.1558-5646.1996.tb03563.x

Gene network robustness as a multivariate character
Genetic and environmental robustness are distinct yet correlated evolvable traits in a gene network
Recommended by Frédéric Guillaume based on reviews by Diogo Melo, Charles Mullon and Charles RocabertOrganisms often show robustness to genetic or environmental perturbations. Whether these two components of robustness can evolve separately is the focus of the paper by Le Rouzic [1]. Using theoretical analysis and individual-based computer simulations of a gene regulatory network model, he shows that multiple aspects of robustness can be investigated as a set of pleiotropically linked quantitative traits. While genetically correlated, various robustness components (e.g., mutational, developmental, homeostasis) of gene expression in the regulatory network evolved more or less independently from each other under directional selection. The quantitative approach of Le Rouzic could explain both how unselected robustness components can respond to selection on other components and why various robustness-related features seem to have their own evolutionary history. Moreover, he shows that all components were evolvable, but not all to the same extent. Robustness to environmental disturbances and gene expression stability showed the largest responses while increased robustness to genetic disturbances was slower. Interestingly, all components were positively correlated and remained so after selection for increased or decreased robustness.
This study is an important contribution to the discussion of the evolution of robustness in biological systems. While it has long been recognized that organisms possess the ability to buffer genetic and environmental perturbations to maintain homeostasis (e.g., canalization [2]), the genetic basis and evolutionary routes to robustness and canalization are still not well understood. Models of regulatory gene networks have often been used to address aspects of robustness evolution (e.g., [3]). Le Rouzic [1] used a gene regulatory network model derived from Wagner’s model [4]. The model has as end product the expression level of a set of genes influenced by a set of regulatory elements (e.g., transcription factors). The level and stability of expression are a property of the regulatory interactions in the network.
Le Rouzic made an important contribution to the study of such gene regulation models by using a quantitative genetics approach to the evolution of robustness. He crafted a way to assess the mutational variability and selection response of the components of robustness he was interested in. Le Rouzic’s approach opens avenues to investigate further aspects of gene network evolutionary properties, for instance to understand the evolution of phenotypic plasticity.
Le Rouzic also discusses ways to measure his different robustness components in empirical studies. As the model is about gene expression levels at a set of protein-coding genes influenced by a set of regulatory elements, it naturally points to the possibility of using RNA sequencing to measure the variation of gene expression in know gene networks and assess their robustness. Robustness could then be studied as a multidimensional quantitative trait in an experimental setting.
References
[1] Le Rouzic, A (2022) Gene network robustness as a multivariate character. arXiv: 2101.01564, ver. 5 peer-reviewed and recommended by Peer Community in Evolutionary Biology. https://arxiv.org/abs/2101.01564
[2] Waddington CH (1942) Canalization of Development and the Inheritance of Acquired Characters. Nature, 150, 563–565. https://doi.org/10.1038/150563a0
[3] Draghi J, Whitlock M (2015) Robustness to noise in gene expression evolves despite epistatic constraints in a model of gene networks. Evolution, 69, 2345–2358. https://doi.org/10.1111/evo.12732
[4] Wagner A (1994) Evolution of gene networks by gene duplications: a mathematical model and its implications on genome organization. Proceedings of the National Academy of Sciences, 91, 4387–4391. https://doi.org/10.1073/pnas.91.10.4387
Trait-specific trade-offs prevent niche expansion in two parasites
Trade-offs in fitness components and ecological source-sink dynamics affect host specialisation in two parasites of Artemia shrimps
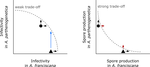
Recommended by Frédéric Guillaume based on reviews by Anne Duplouy, Seth Barribeau and Cindy GidoinEcological specialisation, especially among parasites infecting a set of host species, is ubiquitous in nature. Host specialisation can be understood as resulting from trade-offs in parasite infectivity, virulence and growth. However, it is not well understood how variation in these trade-offs shapes the overall fitness trade-off a parasite faces when adapting to multiple hosts. For instance, it is not clear whether a strong trade-off in one fitness component may sufficiently constrain the evolution of a generalist parasite despite weak trade-offs in other components. A second mechanism explaining variation in specialisation among species is habitat availability and quality. Rare habitats or habitats that act as ecological sinks will not allow a species to persist and adapt, preventing a generalist phenotype to evolve. Understanding the prevalence of those mechanisms in natural systems is crucial to understand the emergence and maintenance of host specialisation, and biodiversity in general. In their study "Trait-specific trade-offs prevent niche expansion in two parasites", Lievens *et al.* [1] report the results of an evolution experiment involving two parasitic microsporidians, *Anostracospora rigaudi* and *Enterocytospora artemiae*, infecting two sympatric species of brine shrimp, *Artemia franciscana* and *Artemia parthenogenetica*. The two parasites were originally specialised on their primary host: *A. rigaudi* on *A. parthenogenetica* and *E. artemiae* on *A. franciscana*, although they encounter both species in the wild but at different rates. After passaging each parasite on each single host and on both hosts alternatively, Lievens *et al.* asked how host specialisation evolved. They found no change in specialisation at the fitness level in *A. rigaudi* in either treatment, while *E. artemiae* became more of a generalist after having been exposed to its secondary host, *A. parthenogenetica*. The most interesting part of the study is the decomposition of the fitness trade-off into its underlying trade-offs in spore production, infectivity and virulence. Both species remained specialised for spore production on their primary host, interpreted as caused by a strong trade-off between hosts preventing improvements on the secondary host. *A. rigaudi* evolved reduced virulence on its primary host without changes in the overall fitness trad-off, while *E. artemiae* evolved higher infectivity on its secondary host making it a more generalist parasite and revealing a weak trade-off for this trait and for fitness. Nevertheless, both parasites retained higher fitness on their primary host because of the lack of an evolutionary response in spore production. This study made two important points. First, it showed that despite apparent strong trade-off in spore production, a weak trade-off in infectivity allowed *E. artemiae* to become less specialised. In contrast, *A. rigaudi* remained specialised, presumably because the strong trade-off in spore production was the overriding factor. The fitness trade-off that results from the superposition of multiple underlying trade-offs is thus difficult to predict, yet crucial to understand potential evolutionary outcomes. A second insight is related to the ecological context of the evolution of specialisation. The results showed that *E. artemiae* should be less specialised than observed, which points to a role played by source-sink dynamics on *A. parthenogenetica* in the wild. The experimental approach of Lievens *et al.* thus allowed them to nicely disentangle the various sources of constraints on the evolution of host adaptation in the *Artemia* system. **References** [1] Lievens, E.J.P., Michalakis, Y. and Lenormand, T. (2019). Trait-specific trade-offs prevent niche expansion in two parasites. bioRxiv, 621581, ver. 4 peer-reviewed and recommended by PCI Evolutionary Biology. doi: [10.1101/621581](https://dx.doi.org/10.1101/621581)
Reviews: 3

Density dependent environments can select for extremes of body size
A population biological modeling approach for life history and body size evolution
Recommended by Wolf Blanckenhorn based on reviews by Frédéric Guillaume and 2 anonymous reviewersBody size evolution is a central theme in evolutionary biology. Particularly the question of when and how smaller body sizes can evolve continues to interest evolutionary ecologists, because most life history models, and the empirical evidence, document that large body size is favoured by natural and sexual selection in most (even small) organisms and environments at most times. How, then, can such a large range of body size and life history syndromes evolve and coexist in nature?
The paper by Coulson et al. lifts this question to the level of the population, a relatively novel approach using so-called integral projection (simulation) models (IPMs) (as opposed to individual-based or game theoretical models). As is well outlined by (anonymous) Reviewer 1, and following earlier papers spearheading this approach in other life history contexts, the authors use the well-known carrying capacity (K) of population biology as the ultimate fitness parameter to be maximized or optimized (rather than body size per se), to ultimately identify factors and conditions promoting the evolution of extreme body sizes in nature. They vary (individual or population) size-structured growth trajectories to observe age and size at maturity, surivorship and fecundity/fertility schedules upon evaluating K (see their Fig. 1). Importantly, trade-offs are introduced via density-dependence, either for adult reproduction or for juvenile survival, in two (of several conceivable) basic scenarios (see their Table 2). All other relevant standard life history variables (see their Table 1) are assumed density-independent, held constant or zero (as e.g. the heritability of body size).
The authors obtain evidence for disruptive selection on body size in both scenarios, with small size and a fast life history evolving below a threshold size at maturity (at the lowest K) and large size and a slow life history beyond this threshold (see their Fig. 2). Which strategy wins ultimately depends on the fitness benefits of delaying sexual maturity (at larger size and longer lifespan) at the adult stage relative to the preceeding juvenile mortality costs, in agreement with classic life history theory (Roff 1992, Stearns 1992). The modeling approach can be altered and refined to be applied to other key life history parameters and environments. These results can ultimately explain the evolution of smaller body sizes from large body sizes, or vice versa, and their corresponding life history syndromes, depending on the precise environmental circumstances.
All reviewers agreed that the approach taken is technically sound (as far as it could be evaluated), and that the results are interesting and worthy of publication. In a first round of reviews various clarifications of the manuscript were suggested by the reviewers. The new version was substantially changed by the authors in response, to the extent that it now is a quite different but much clearer paper with a clear message palatable for the general reader. The writing is now to the point, the paper's focus becomes clear in the Introduction, Methods & Results are much less technical, the Figures illustrative, and the descriptions and interpretations in the Discussion are easy to follow.
In general any reader may of course question the choice and realism of the scenarios and underlying assumptions chosen by the authors for simplicity and clarity, for instance no heritability of body size and no cost of reproduction (other than mortality). But this is always the case in modeling work, and the authors acknowledge and in fact suggest concrete extensions and expansions of their approach in the Discussion.
References
Coulson T., Felmy A., Potter T., Passoni G., Montgomery R.A., Gaillard J.-M., Hudson P.J., Travis J., Bassar R.D., Tuljapurkar S., Marshall D.J., Clegg S.M. (2022) Density-dependent environments can select for extremes of body size. bioRxiv, 2022.02.17.480952, ver. 3 peer-reviewed and recommended by Peer Community in Evolutionary Biology. https://doi.org/10.1101/2022.02.17.480952
A demogenetic agent based model for the evolution of traits and genome architecture under sexual selection
Sexual selection goes dynamic
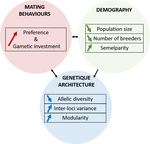
Recommended by Michael D Greenfield based on reviews by Frédéric Guillaume and 1 anonymous reviewer150 years after Darwin published ‘Descent of man and selection in relation to sex’ (Darwin, 1871), the evolutionary mechanism that he laid out in his treatise continues to fascinate us. Sexual selection is responsible for some of the most spectacular traits among animals, and plants, and it appeals to our interest in all things reproductive and sexual (Bell, 1982). In addition, sexual selection poses some of the more intractable problems in evolutionary biology: Its realm encompasses traits that are subject to markedly different selection pressures, particularly when distinct, yet associated, traits tend to be associated with males, e.g. courtship signals, and with females, e.g. preferences (cf. Ah-King & Ahnesjo, 2013). While separate, such traits cannot evolve independently of each other (Arnqvist & Rowe, 2005), and complex feedback loops and correlations between them are predicted (Greenfield et al., 2014). Traditionally, sexual selection has been modelled under simplifying assumptions, and quantitative genetic approaches that avoided evolutionary dynamics have prevailed. New computing methods may be able to free the field from these constraints, and a trio of theoreticians (Chevalier, De Coligny & Labonne 2020) describe here a novel application of a ‘demo-genetic agent (or individual) based model’, a mouthful hereafter termed DG-ABM, for arriving at a holistic picture of the sexual selection trajectory. The application is built on the premise that traits, e.g. courtship, preference, gamete investment, competitiveness for mates, can influence the genetic architecture, e.g. correlations, of those traits. In turn, the genetic architecture can influence the expression and evolvability of the traits. Much of this influence occurs via demographic features, i.e. social environment, generated by behavioral interactions during sexual advertisement, courtship, mate guarding, parental care, post-mating dispersal, etc.
The authors provide a lengthy verbal description of their model, specifying the genomic and behavioral parameters that can be set and how a ‘run’ may be initialized. There is a link to an internet site where users can then enter their own parameter values and begin exploring hypotheses. Back in the article several simulations illustrate simple tests; e.g. how gamete investment and preference jointly evolve given certain survival costs. One obvious test would have been the preference – courtship genetic correlation that represents the core of Fisherian runaway selection, and it is regrettable that it was not examined under a range of demographic parameters. As presented the author’s DG-ABM appears particularly geared toward mating systems in ‘higher’ vertebrates, where couples form during a discrete mating season and are responsible for most reproduction. It is not clear how applicable the model could be to a full range of mating systems and nuances, including those in arthropods and other invertebrates as well as plants.
What is the likely value of the DG-ABM for sexual selection researchers? We will not be able to evaluate its potential impact until readers with specialized understanding of a question and taxon begin exploring and comparing their results with prior expectations. Of course, lack of congruence with earlier predictions would not invalidate the model. Hopefully, some of these specialists will have opportunities for comparing results with pertinent empirical data.
References
Ah-King, M. and Ahnesjo, I. 2013. The ‘sex role’ concept: An overview and evaluation Evolutionary Biology, 40, 461-470. doi: https://doi.org/10.1007/s11692-013-9226-7
Arnqvist, G. and Rowe, L. 2005. Sexual Conflict. Princeton University Press, Princeton. doi: https://doi.org/10.1515/9781400850600
Bell, G. 1982. The Masterpiece of Nature: The Evolution and Genetics of Sexuality. University of California Press, Berkeley.
Chevalier, L., De Coligny, F. and Labonne, J. (2020) A demogenetic individual based model for the evolution of traits and genome architecture under sexual selection. bioRxiv, 2020.04.01.014514, ver. 4 peer-reviewed and recommended by PCI Evol Biol. doi: https://doi.org/10.1101/2020.04.01.014514
Darwin, C. 1871. The Descent of Man and Selection in Relation to Sex. J. Murray, London.
Greenfield, M.D., Alem, S., Limousin, D. and Bailey, N.W. 2014. The dilemma of Fisherian sexual selection: Mate choice for indirect benefits despite rarity and overall weakness of trait-preference genetic correlation. Evolution, 68, 3524-3536. doi: https://doi.org/10.1111/evo.12542
Effects of partial selfing on the equilibrium genetic variance, mutation load and inbreeding depression under stabilizing selection
Understanding genetic variance, load, and inbreeding depression with selfing
Recommended by Aneil F. Agrawal based on reviews by Frédéric Guillaume and 1 anonymous reviewerA classic problem in evolutionary biology is to understand the genetic variance in fitness. The simplest hypothesis is that variation exists, even in well-adapted populations, as a result of the balance between mutational input and selective elimination. This variation causes a reduction in mean fitness, known as the mutation load. Though mutation load is difficult to quantify empirically, indirect evidence of segregating genetic variation in fitness is often readily obtained by comparing the fitness of inbred and outbred offspring, i.e., by measuring inbreeding depression. Mutation-selection balance models have been studied as a means of understanding the genetic variance in fitness, mutation load, and inbreeding depression. Since their inception, such models have increased in sophistication, allowing us to ask these questions under more realistic and varied scenarios. The new theoretical work by Abu Awad and Roze [1] is a substantial step forward in understanding how arbitrary levels of self-fertilization affect variation, load and inbreeding depression under mutation-selection balance.
It has never been entirely clear how selfing should affect these population genetic properties in a multi-locus model. From the single-locus perspective, selfing increases homozygosity, which allows for more efficient purging leading to a prediction of less variance and lower load. On the other hand, selfing directly and indirectly affects several types of multilocus associations, which tend to make selection less efficient. Though this is certainly not the first study to consider mutation-selection balance in species with selfing (e.g., [2-5]), it is perhaps the most biologically realistic. The authors consider a model where n traits are under stabilizing selection and where each locus affects an arbitrary subset of these traits. As others have argued [6-7], this type of fitness landscape model “naturally” gives rise to dominance and epistatic effects. Abu Awad and Roze [1] thoroughly investigate this model both with analytical approximations and stochastic simulations (incorporating the effects of drift).
Their analysis reveals three major parameter regimes. The first regime occurs under low mutation rates, when segregating deleterious alleles are sufficiently rare across the genome that multi-locus genetic associations (disequilibria) can be ignored. As expected, in this regime, increased selfing facilitates purging, thereby leading to less standing genetic variation, lower load and less inbreeding depression.
In the second regime, mutation rates are higher and segregating deleterious alleles are more common. Though the effects of multilocus genetic associations cannot be ignored, Abu Awad and Roze [1] show that a good approximation can be obtained by considering only two-locus associations (ignoring the multitude of higher order associations). This is where the sophistication of their analysis yields the greatest insights. Their analysis shows that two different types of interlocus associations are important. First, selfing directly generates identity disequilibrium (correlation in homozygosity between two loci) that occurs because individuals produced through outbreeding tend to be heterozygous across multiple loci whereas individuals produced by selfing tend to be homozygous across multiple loci. These correlations reduce the efficiency of selection when deleterious effects are partially recessive [5]. Second, selfing indirectly affects traditional linkage disequilibrium. Epistatic selection resulting from the fitness landscape generates negative linkage disequilibrium between alleles at different loci that cause the same direction of deviation in a trait from its optimum. Because selfing reduces the effective rate of recombination, linkage disequilibrium reaches higher levels. Because selection tends to generate compensatory combinations of alleles, partially masking their deleterious effects, these associations also make purging less efficient. Their analysis shows the strength of the effect from identity disequilibrium scales with U, the genome-wide rate of deleterious mutations, but the effect of linkage disequilibrium scales with U/n because with more traits (higher n) two randomly chosen alleles are less likely to affect the same trait and so be subject to epistatic selection. Together, the effects of multilocus associations increase the load and can, in some cases, cause the load to increase as selfing increase from moderate to high levels.
However, their analytical approximations become inaccurate under conditions when the number of epistatically interacting segregating mutations (proportional to U/n) becomes large relative to the effective recombination rate (dependent on outcrossing and recombination rates). In this third regime, higher order genetic associations become important. In the limit of no recombination, model behaves as if the whole genome is a single locus with a very large number of alleles, becoming equivalent to previous studies [2-3].
The study by Abu Awad and Roze [1] helps us better understand the “simplest” explanation for genetic variance in fitness—mutation-selection balance—in a model of considerable complexity involving multiple traits under stabilizing selection, which ‘naturally’ allows for pleiotropy and epistasis. Their model tends to confirm the classic prediction of lower variation in fitness, less load, and inbreeding depression in species with higher levels of selfing. However, their careful analysis provides a clearer picture of how (and by how much) epistasis and selfing affect key population genetic properties.
References
[1] Abu Awad D and Roze D. 2017. Effects of partial selfing on the equilibrium genetic variance, mutation load and inbreeding depression under stabilizing selection. bioRxiv, 180000, ver. 4 of 17th November 2017. doi: 10.1101/180000
[2] Lande R. 1977. The influence of the mating system on the maintenance of genetic variability in polygenic characters. Genetics 86: 485–498.
[3] Charlesworth D and Charlesworth B. 1987. Inbreeding depression and its evolutionary consequences. Annual Review of Ecology and Systematics. 18: 237–268. doi: 10.1111/10.1146/annurev.es.18.110187.001321
[4] Lande R and Porcher E. 2015. Maintenance of quantitative genetic variance under partial self-fertilization, with implications for the evolution of selfing. Genetics 200: 891–906. doi: 10.1534/genetics.115.176693
[5] Roze D. 2015. Effects of interference between selected loci on the mutation load, inbreeding depression, and heterosis. Genetics 201: 745–757. doi: 10.1534/genetics.115.178533
[6] Martin G and Lenormand T. 2006. A general multivariate extension of Fisher's geometrical model and the distribution of mutation fitness effects across species. Evolution 60: 893–907. doi: 10.1111/j.0014-3820.2006.tb01169.x
[7] Martin G, Elena SF and Lenormand T. 2007. Distributions of epistasis in microbes fit predictions from a fitness landscape model. Nature Genetics 39: 555–560. doi: 10.1038/ng1998