
A general model of fitness effects following hybridisation
How does the mode of evolutionary divergence affect reproductive isolation?
Abstract
Recommendation: posted 19 December 2022, validated 20 December 2022
Hartfield, M. (2022) A general model of fitness effects following hybridisation. Peer Community in Evolutionary Biology, 100543. https://doi.org/10.24072/pci.evolbiol.100543
Recommendation
Studying the effects of speciation, hybridisation, and evolutionary outcomes following reproduction from divergent populations is a major research area in evolutionary genetics [1]. There are two phenomena that have been the focus of contemporary research. First, a classic concept is the formation of ‘Bateson-Dobzhansky-Muller’ incompatibilities (BDMi) [2–4] that negatively affect hybrid fitness. Here, two diverging populations accumulate mutations over time that are unique to that subpopulation. If they subsequently meet, then these mutations might negatively interact, leading to a loss in fitness or even a complete lack of reproduction. BDMi formation can be complex, involving multiple genes and the fitness changes can depend on the direction of introgression [5]. Second, such secondary contact can instead lead to heterosis, where offspring are fitter than their parental progenitors [6].
Understanding which outcomes are likely to arise require one to know the potential fitness effects of mutations underlying reproductive isolation, to determine whether they are likely to reduce or enhance fitness when hybrids are formed. This is far from an easy task, as it requires one to track mutations at several loci, along with their effects, across a fitness landscape.
The work of De Sanctis et al. [7] neatly fills in this knowledge gap, by creating a general mathematical framework for describing the consequences of a cross from two divergent populations. The derivations are based on Fisher’s Geometric Model, which is widely used to quantify selection acting on a general fitness landscape that is affected by several biological traits [8,9], and has previously been used in theoretical studies of hybridisation [10–12]. By doing so, they are able to decompose how divergence at multiple loci affects offspring fitness through both additive and dominance effects.
A key result arising from their analyses is demonstrating how offspring fitness can be captured by two main functions. The first one is the ‘net effect of evolutionary change’ that, broadly defined, measures how phenotypically divergent two populations are. The second is the ‘total amount of evolutionary change’, which reflects how many mutations contribute to divergence and the effect sizes captured by each of them. The authors illustrate these measurements using simulations covering different scenarios, demonstrating how different parental states can lead to similar fitness outcomes. They also propose experimental methods to measure the underlying mutational effects.
This study neatly demonstrates how complex genetic phenomena underlying hybridisation can be captured using fairly simple mathematical formulae. This powerful approach will thus open the door for future research to investigate hybridisation in more detail, whether it is by expanding on these theoretical models or using the elegant outcomes to quantify fitness effects in experiments.
References
1. Coyne JA, Orr HA. Speciation. Sunderland, Mass: Sinauer Associates; 2004.
2. Bateson W, Seward A. Darwin and modern science. Heredity and variation in modern lights. 1909;85: 101. https://doi.org/10.1017/CBO9780511693953.007
3. Dobzhansky T. Genetics and the Origin of Species. Columbia university press; 1937.
4. Muller HJ. Isolating mechanisms, evolution and temperature. Biol Symp. 1942;6: 71-125.
5. Fraïsse C, Elderfield JAD, Welch JJ. The genetics of speciation: are complex incompatibilities easier to evolve? J Evol Biol. 2014;27: 688-699. https://doi.org/10.1111/jeb.12339
6. Birchler JA, Yao H, Chudalayandi S, Vaiman D, Veitia RA. Heterosis. The Plant Cell. 2010;22: 2105-2112. https://doi.org/10.1105/tpc.110.076133
7. De Sanctis B, Schneemann H, Welch JJ. How does the mode of evolutionary divergence affect reproductive isolation? bioRxiv. 2022. 2022.03.08.483443 version 4. https://doi.org/10.1101/2022.03.08.483443
8. Fisher RA. The genetical theory of natural selection. Oxford: The Clarendon Press; 1930. https://doi.org/10.5962/bhl.title.27468
9. Tenaillon O. The Utility of Fisher's Geometric Model in Evolutionary Genetics. Annu Rev Ecol Evol Syst. 2014;45: 179-201. https://doi.org/10.1146/annurev-ecolsys-120213-091846
10. Barton NH. The role of hybridization in evolution. Molecular Ecology. 2001;10: 551-568. https://doi.org/10.1046/j.1365-294x.2001.01216.x
11. Chevin L-M, Decorzent G, Lenormand T. Niche Dimensionality and The Genetics of Ecological Speciation. Evolution. 2014;68: 1244-1256. https://doi.org/10.1111/evo.12346
12. Fraïsse C, Gunnarsson PA, Roze D, Bierne N, Welch JJ. The genetics of speciation: Insights from Fisher's geometric model. Evolution. 2016;70: 1450-1464. https://doi.org/10.1111/evo.12968
The recommender in charge of the evaluation of the article and the reviewers declared that they have no conflict of interest (as defined in the code of conduct of PCI) with the authors or with the content of the article. The authors declared that they comply with the PCI rule of having no financial conflicts of interest in relation to the content of the article.
BDS and HS acknowledge support from the Wellcome Trust program in Mathematical Genomics and Medicine (WT220023 and RG92770)
Evaluation round #2
DOI or URL of the preprint: https://www.biorxiv.org/content/10.1101/2022.03.08.483443v3
Version of the preprint: 3
Author's Reply, 07 Dec 2022
Decision by Matthew Hartfield, posted 02 Dec 2022, validated 02 Dec 2022
Many thanks for your substantial revisions of this preprint. Both reviewers and myself find this new version more comprehensive than before, and appreciate the effort made into improving the clarity of these complex analyses. That said, given the large amount of changes that have been made (to me it felt a bit like reading a whole new paper), there are still several suggestions that were made for improving the manuscript and its clarity. I hence feel it is worth further revising the manuscript before it can be recommended by PCI, but I foresee that it would not be sent out for further reviews after the next submission.
I have a few additional comments to add:
- I feel the two functions m, M could be defined earlier, when Figure 1 is introduced. I found it difficult to fully understand Figure 1 on a first read, as it makes references to these functions but they were not yet defined in the text. I think it would be sufficient to simply define the mathematical functions here, and leave the interpretation section in the same location.
- Line 178: missing full stop (or other punctuation mark) at the end of this sentence.
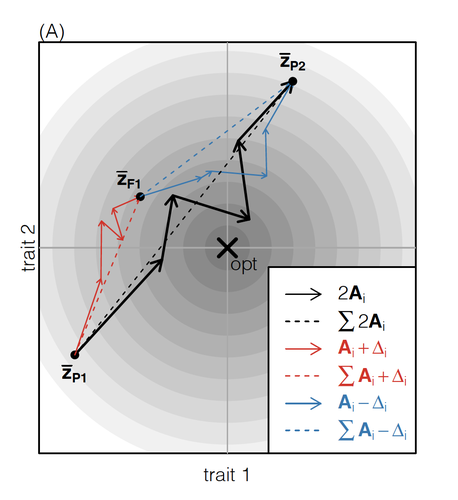
- Figure 2: It's not clear to me what the big and little arrows represent in the 'Divergence scenarios' box. Furthermore I do not understand why there is a big arrow coming from P1 if only P2 moves in this case?
Reviewed by Luis-Miguel Chevin, 17 Nov 2022
This revision is a very different manuscript from the first submission, somewhat unexpectedly as the previous round of reviews were quite positive. The analysis has been extended in a number of ways, mostly by allowing polymorphism in parental populations, such that what used to be expressed in terms of phenotypic effects and frequencies (in hybrids) of alleles fixed in each parental population now appears as components of variance typical of quantitative genetics partitioning (additive, dominance, etc), which accounts for polymorphism. The explored evolutionary scenarios are also partly different, not only regarding directional selection, but also by including a detailed exploration of drift around a constant optimum (described as stabilizing selection). As a consequence, (almost) all the figures have changed, and so has the text. I praise the authors for this effort, which has undoubtedly made the manuscript richer, and even more interesting than it was. On the other hand, this density of results also certainly makes it a difficult read, more so than the previous version. I can’t say I’ve digested all results myself as much as I would have liked, when it comes to contrasting net evolution to total evolution for interactions between additive and dominance terms, under different scenarios of dominance at the phenotypic level (Figure 4). Still, I can’t find any obvious way around this: the authors have pursued a thorough analysis of the model while keeping it rather general (not assuming fixation in parental populations, additivity at phenotypic level, etc), so they just have lots of things to say, some of which are not straightforward. They have done some efforts to synthetize their results in Table 4, and suggest ways to empirically assess some of their predictions. Some presentation choices don’t facilitate understanding in my opinion (such as the absence of an explicit ancestral phenotype, instead using directional flow of mutations from P1 to P2), but this has been discussed previously and the authors have their arguments for doing things this way. So I will just list a few minor points below.
Minor points:
12: ‘making fewer assumptions’ than what? Please specify
44: perhaps insert ‘before hybrids form’ after ‘that have accumulated”
144: Perhaps write “sum of phenotypic variances among traits” instead of “sum of the trait variances”, as the latter could mean different things, including sum across loci for a given trait.
Figure 2: The cartoons on the left are far from being self-evident. For instance, what’s the difference between light and dark colors for the thick arrow? I can only guess that this relates to which population evolves, but the precise meaning isn’t obvious. And what about the small thin arrows attached to the thick ones? Why are they not described in the caption?
314: I think you mean VI and not IV here.
Eq 42, second line for P_BB,i: one of the terms in the difference in parentheses should harbour P_1 instead of P_2, otherwise this term vanishes
652: typo ‘phenoptypic’
656: ‘positive epistasis in an optimal background’. Note that epistasis does not depend on genetic background, but only on mutation phenotypic effects, in this classic quadratic/Gaussian version of FGM
https://doi.org/10.24072/pci.evolbiol.100543.rev21Reviewed by Juan Li, 31 Oct 2022
The authors have greatly improved their clarity. Thank the authors for clarifying the epistasis in Appendix 1. In this version, my remaining comments are limited to clarifications.
I appreciate the authors’ effort in including the segregating sites mathematically. However, some significant results come from simulations, and the author used divergence between populations to demonstrate. This makes me wonder about the reason for using shared polymorphism. How should we understand the contribution of shared polymorphism and fixed differences to hybrids or to postzygotic RI? Are they the same in two species? And how much of the shared polymorphism do we expect from two species? Since the authors and reviewer Chevin have discussed this, I hope the authors could explain a bit, like explicitly writing a paragraph in the introduction or method.
Abstract – In general, “The key quantities” include two properties of the evolution changes and their interactions, right? This term is not obvious to me.
Table 6 and page 21 -- I am confused with the inbreeding coefficient in the F1 population. If the two parental populations perform random mating to form the F1 hybrid population, the inbreeding coefficient is 0 in the F1 population (HWE). If the F1 population contains only hybrids of two populations, the F1 population is a result of complete assortative mating (“an excess of heterozygotes”).
Table 6, eq. 6, eq. 32, eq. 33. -- I am confused with d_ij and delta_ij. Are they describing the same thing, the dominance in Table 5? Or is delta_ij about dominance at the population level? Is the dominance defined at a single locus (Table 5) equal to the mean dominance (eq. 33)?
Eq. 49 – Please notice that the equation is too large to show on one line.
Figure 2 – The black circle is the ancestry population, shown in the panel illustrating scenario I. I guess that the center of each panel is not the optimum (the cross in figure 1), but the two dots are two optima. I guess that the large arrow indicates the direction of additive effects, and the small arrow indicates the dominance. It might be helpful to clarify this in the figure legend.
Figure 4 – I suggest the authors keep the panels to describe two scenarios of stabilizing selection (in old Figure 2, like the left panels in new Figure 2). It makes it easier to understand a theoretical paper.
Line 321 – “Unlike terms involving additive or dominance effects alone, the interaction terms capture differences in the evolutionary changes between two populations.” The word, “differences”, is not clear to me. Throughout the whole section, the author explains how dominance affects the fixation of mutations, Haldane’s Sieve. Maybe, rephrase this sentence?
https://doi.org/10.24072/pci.evolbiol.100543.rev22Evaluation round #1
DOI or URL of the preprint: https://doi.org/10.1101/2022.03.08.483443
Author's Reply, 11 Oct 2022
Please see the uploaded pdf for a response to reviewers. We would like to note that, other than the abstract and introduction, nearly every word in the manuscript has been changed, so we recommend reading the new version instead of the one with tracked changes.
Decision by Matthew Hartfield, posted 30 May 2022
Your manuscript has been assessed by two reviewers. Both find this a good and insightful investigation into how the form form of divergence influences reproduction isolation, and I agree. This manuscript has potential to be recommended by PCI Evolutionary Biology, but the reviewers have made several suggestions for revisions. I have made a few myself that I list below, but note that most suggestions revolve around improving the clarity of the manuscript rather than substantial methodological changes.
My additional comments below:
- I would like a bit more information on the model assumptions regarding how the two parental individuals diverge in the first place, and how they relate to the MRCA. I presume that, sometime in the past, there was an ancestral individual in a well-mixed population (the MRCA individual), whose offspring started diverging genetically, leading to the two parental individuals P1 and P2. Hence, the fixed genetic differences (of which there are D of them) are given relative to this ancestral individual. Is that the case? I also assume that the MRCA can be located anywhere in fitness space (as suggested in Figure 1), and not necessarily at the optimum (as is mostly simulated in Figure 2)? Clarifying these starting assumptions will help the reader better understand the biological process that are being modelled.
- It would be easier to understand Figure 2 if the different scenarios were explained first, before the figure is discussed in depth on pages 6-8. These scenarios are eventualy explained over the subsequent few pages, but on first reading it is unclear what is being investigated and hence how they affect the quantities being studied.
- Eq. 26: Could you clarify what is meant by the notation 'if lnwP1 = 0 or lnwP2 = 0'? If applied literally then this equation would reduce to the absolute value of the non-zero term and does not need to be spelt out in full.
- Line 312: Unclear what is meant by "heterozygosity has little impact on the results" as it does not appear that heterozygosity has been investigated in Figure 3.
- In the simulations, it is unclear what is meant when selection and dominance effects have 'vanishing' parameters (on lines 455 and 458). Perhaps it would be better to write out the distributions in full?
Best regards,
Matthew Hartfield
Reviewed by Luis-Miguel Chevin, 19 Apr 2022
In this manuscript, De Sanctis et al investigate how the mode of divergence between parental populations affects the fitness of their hybrids across environments. The mode of divergence encompasses the phenotypic direction of evolution from the most recent common ancestor (MRCA), as well as the phenotypic effects of mutations that fixed, both in terms of magnitude (additive effects) and within-locus interactions (dominance effects). In line with previous work on this question, starting from Barton (2001) and followed up by a series of papers in the last decade (including several by their group), they model adaptation using Fisher’s geometrical model (FGM), whereby fitness depends on squared phenotypic distances from the optimum at multiple traits. Using this common baseline, they rely on combinatorics to generalize and extend previous findings about the way evolutionary trajectories of parental populations influence the fitness of their hybrids.
One of their main insights is that all outcomes regarding hybrids fitness, including the relative contributions of intrinsic vs extrinsic (environment-dependent) isolation, essentially depend on two evolutionary metrics: the total amount of evolutionary change, which sums the squared magnitudes of all mutation effects, and the net effect of evolutionary change, which is the squared magnitude of the overall change (which itself sums all mutation effects). These two metrics, which can be applied to additive and dominance effects, summarize complementary aspects of the evolutionary trajectories of parental populations. When combined with summaries of the genetic composition of hybrids (hybrid index, proportion of heterozygous sites, etc), they are sufficient to predict their expected (log) fitness. The authors provide complementary interpretations of their results in terms of geometry in phenotypic space, and of selection coefficients and epistasis.
The work presented in this ms is an interesting and useful extension of previous theory on this topic, providing insightful general explanations that clarify and unify earlier findings, as well as exploring a larger diversity of evolutionary scenario. The analysis seems solid, therefore I have no major criticisms, but rather suggestions for improvement of presentation.
First, some arguments made here appeared in simpler forms in earlier work, which could perhaps be credited a bit more for completeness. For instance, the difference between the squared total phenotypic change (“net effect of evolutionary change here”) vs sum of squared changes (“total amount of evolutionary change”), and how this relates to fitness epistasis and the angle between mutations, was a key step in the derivations and overall argument in Chevin et al (2014), although perhaps a bit cryptically (between eq. 3 and appendix S1 of that paper, in a non-isotropic model where distances are less directly meaningful and are thus translated into fitness effects), and restricted to a scenario of directional selection akin to that explored in the last section and Figure 3 of the current ms. Some results about mutation-selection-drift equilibrium around a constant optimum, and the partitioning between intrinsic and extrinsic isolation, also seemed quite similar to points made here, after accounting for the fact that the “total amount of evolutionary change” is very much related to the segregation variance (including regarding the contrasted effects of a few large vs many small mutations, in fig 3 of the present ms). This is not to say that the results here are not novel or insightful, but rather that it may be worthwhile relating them a bit more explicitly to work that touched on very similar issues in a less general way, so as to clarify the improvements made here.
Regarding the model per se, perhaps I haven’t read it carefully enough, but after several attempts I have been unable to find a proper description of what y represents in the g(x,y) functions (and S_xy in the methods). Since this function is a crucial component of hybrid fitness, it is important to be very explicit about it, to avoid any confusion or wrong interpretations. From my reading and previous understanding of these models, I concluded that x and y correspond to mutations that originate from the two different parental backgrounds, but I can’t be sure about that.
Another point of definition that was not very clear to me was about the angle theta between substitution vectors. The first time this topic of orientation is brought up in the ms, I found it quite confusing to read (below eq. 16) that “we have cos(theta) = -1 when two substitutions point in the same phenotypic direction (such that theta = pi), […] and cos(theta) = 1 for substitutions that point in opposite directions”, because this seems to contradict basic trigonometry, if theta is the angle between two vectors. Only when looking more carefully at fig 1B did I realize that theta was in fact not the angle between the two vectors under consideration, but rather pi minus this angle (ie, the supplementary angle, as stated much later in the ms). It is unclear to me why theta was defined in this way, and I think this can be confusing to many readers used to applying geometric arguments to phenotypic spaces. If the goal was just to eliminate a minus sign before the scalar products, at the moment this seems to be done at the expense of the intuitive meaning, which is regrettable since intuitive interpretation seems to be one of the key goals of this paper. I would find it simpler to keep the minus sign in the formulas and rely on the actual angle between vectors, such that these formulas would state that something about the relative orientation of mutations is subtracted from the rest. If not using this option, then the authors should at least state clearly that theta is not the angle between vectors as usually defined, but the supplement to that angle, and provide an intuitive explanation for why that is (as it does not seem sufficient to just write that “the negative sign comes from the need to take the supplementary angle due to the directionality of the vectors”).
Minor comments
22 : “Genomic and phenotypic differentiation between populations is a major cause” -> “are”?
44-45: “strong assumptions about the distribution of the fixed effects (e.g., normality, universal pleiotropy, and independence among traits)”. Normality is often assumed for the phenotypic distribution of mutation effects, but not for fixed effects; and at least one model of hybrid fitness in FGM (the one I know best, cited above) did allow for correlations among traits.
120-121: “describes interactions between heterospecic alleles in different states”. Perhaps state here (if relevant) that you are referring to additive-by-additive or additive-by-dominance epistasis for fitness?
Eqs below 402 (methods): A key implicit step in this derivation (which is central to the results in the ms) is the requirement that the probability for a locus to be in each genetic state (heterozygote or each homozygote) does not covary with allelic phenotypic effect. I would find it useful to state this explicitly for completeness, and to explain what this implies: probably something quite general like fair segregation, or rather phenotype-independent segregation?
Eq below 409: For those curious about that (including me!), could you explain where this product of binomial coefficients comes from?
Figure S1: I can't help noticing a substantial effect of phenotypic dimensionality n, mostly on the net effect m(2a), and to a lesser extent on the total amount M(2a) of evolutionary change (comparing triangles with circles), and thus on hybrid fitness. I tend to think that this is worth mentioning briefly in the ms, but this may be a personal bias!
https://doi.org/10.24072/pci.evolbiol.100543.rev11Reviewed by Juan Li, 29 Apr 2022
The manuscript “How does the mode of evolutionary divergence affect reproductive isolation?” is an explicit, well-written manuscript on the evolution of reproductive isolation (RI) under Fisher’s geometric model. This paper aimed to investigate the connections between genotype and phenotype to explain the fitness of hybrids, from which we could gain an insight into the strength of reproductive isolation. Here, they presented the total amount (intrinsic, related to genotype divergence) and net effect (extrinsic, related to phenotype distribution) of evolutionary change caused by additive and dominance effects and their interactions. Using simulations, they showed the distribution of additive and dominance effects under different modes of evolutionary divergence, which result in predictable consequences for the hybrid fitness. They also compared the effect of intrinsic and extrinsic isolation on speciation. Within this scope, they articulate the evolutionary role of large- and weak- effect substitutions on adaptative trajectory and speciation. Based on these conclusions, they generalized their model to the effect of gene flow between species. I enjoyed reading this paper, and I found that the authors balanced the considerable number of equations and their evolutionary interpretation very well. Overall, this is interesting research and presented clearly.
My comments are extremely limited. I offer a few questions to be clarified. Hopefully, the authors could make their theoretical work not limited to being read by theoreticians but more understandable for a broader readership.
Paragraph “Dominance effects” (line 188) – I do not understand the complementary information from additive and dominance effects. In both this paragraph and the discussion (Line 367-Lin 376), the overall dominance reflects the position of the MRCA on the graph, however, it is not related to the additive effect, like, Scenario I and II. Should I expect some explanations from g(a,d) eq. 22? It would be great if the authors could make this connection more clear in a revised manuscript.
Figure 3 – 1. I am aware that dominance is assumed to be 0 in the main text. It would be good to spell this out as well in the legend. 2. I can roughly understand the y-axis label, (E(ln wH))/m(2a) in panels A and B, to compare with M(a)/m(a). However, I do not understand why to intuitively scale log fitness by m(2a), i.e., the biological explanation.
Equation 29—It is not obvious for me to get eq. 29 from eq. 19. It would be great if they authors could explain this in a bit more detail in a revised manuscript or provide citations if it has already been analyzed in other papers.
Line 243—Should Figure 1C be Figure 1B? Figure 1C demonstrates F1 and mid-parent, whereas Line 243 pointed to two parental phenotypes.
Section 1.3.3 -- I might misunderstand the purpose of this section. I want to communicate more on eq. 26. I understand that epistasis was defined in eq. 25 from eq. 1 and the fitness effect was an approximation. In this section, dominance was not considered because only homozygous substitutions are present in the background. Meanwhile, the whole manuscript focused on the fitness of hybrids (RI). I am confused with the dominance effect when using the epistatic components in m(2a). Here, the epistatic effect could come from any non-linear genotype-phenotype-fitness map. The epistasis could also be generated on the evolutionary trajectory, meaning a similar epistatic factor is in m(2d). It would be helpful if the authors could explain the meaning and relationship of epistasis in hybrids and when two homozygous substitutions are present in one genome.
Line 548 – This citation seems incomplete. It might be worth checking the reference list.
Overall, I found this an interesting paper that will undoubtedly stimulate people to think about the strength of reproductive isolation and the evolutionary trajectory to RI during adaptation and speciation.
https://doi.org/10.24072/pci.evolbiol.100543.rev12











The BDM acronym might be better referred to as "DM" since B was opposed to the genic viewpoint of D & M. See Forsdyke (2011) Heredity 106, 202.